Алгебраические критерии устойчивости

Главное достоинство алгебраических критериев – возможность получать условия устойчивости в аналитической форме, что очень важно на этапе синтеза закона управления и выбора структуры и параметров корректирующих звеньев.

Критерий Стодолы

Критерий Стодолы определяет необходимые условия устойчивости: для того, чтобы система была устойчивой, необходимо, чтобы все коэффициенты характеристического полинома были одного знака (положительны при a ₀ > 0): a_i > 0 для всех i = 1… n.

Критерий Гурвица

Критерий Гурвица определяет необходимые и достаточные условия устойчивости. Из коэффициентов характеристического полинома

Q (l) = a ₀l ⁿ + a ₁l ^{n -1}+…+ a_n

составляется матрица Гурвица. Это квадратная матрица размером [ n ´ n ]. По главной диагонали — от левого верхнего до правого нижнего угла выписываются все коэффициенты по порядку от a ₁ до a_n. Каждая строка заполняется коэффициентами с возрастанием индекса слева направо: в нечетных строках — коэффициенты с нечетными индексами, в четных строках – с четными индексами. Несуществующие коэффициенты заменяются нулями.

Формулировка критерия: для устойчивости системы необходимо и достаточно, чтобы все определители Гурвица (определители клеточных матриц, построенные на главной диагонали) были одного знака. При a ₀ > 0: D _i > 0, i =1… n. В частности, при

· n = 1: D₁= a ₁ > 0 Þ для систем первого порядка a ₀, a ₁ > 0;

· n = 2: D₂ = a ₁ a ₂ > 0 Þ для систем второго порядка a ₀, a ₁ , a ₂ > 0;

· n = 3: a ₀ > 0 – всегда можно сделать, умножив Q (l) на -1;

D₁ = a ₁ > 0; D₂ = a ₁ a ₂ – a ₀ a ₃ > 0, D₃ = a ₃D₂ >0 Þ для систем третьего порядка a ₀, a ₁, a ₂, a ₃ > 0 и a ₁ a ₂ – a ₀ a ₃ > 0.

Замечание. Условие определения границы устойчивости D _n = 0 распадается на два условия: a_n = 0 и D _{n -1} = 0.

Диаграмма Вышнеградского

Ива́н Алексе́евич Вышнегра́дский (20.12.1831 — 25.03.1895) — русский ученый (специалист в области механики) и государственный деятель. Основоположник теории автоматического регулирования, почетный член Петербургской АН, в 1887—1892 — министр финансов России.

И.А. Вышнеградский в 1876 г. задолго до появления критерия Гурвица (1895 г.) сформулировал условия устойчивости системы третьего порядка, построил диаграмму Вышнеградского (рис. 2.36). Эта работа положила начало развитию теории автоматического управления.

Рис. 2.36. Диаграмма Вышнеградского

Диаграмма показывает область устойчивости и характер расположения корней внутри каждой из частей области устойчивости.

Рассмотрим характеристическое уравнение третьего порядка

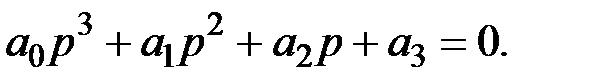
Разделив все члены уравнения на а₃ и введя новую переменную , ,

можно привести уравнение к нормированному виду

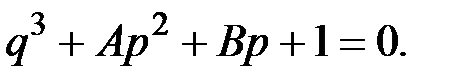
Коэффициенты этого уравнения – параметры Вышнеградского.

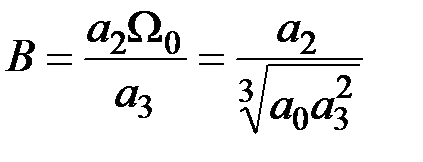
На плоскости параметров А и В условия устойчивости принимают вид: А > 0, В > 0 и АВ >1. Область устойчивости системы лежит выше кривой АВ = 1 при А>0 и В >0. Это равнобокая гипербола, для которой оси координат служат асимптотами.

В области III, где все корни вещественные, в зависимости от начальных условий получим апериодический переходный процесс в одной из форм, показанных на третьем графике рис. 2.37. Область III носит название области апериодических процессов. В областях I и II, где имеется один вещественный корень и два комплексных, переходный процесс будет иметь соответственно формы, показанные на первых двух графиках рис. 2.37.

Рис. 2.37. Характер переходных процессов

В области I быстрее затухает экспонента и переходный процесс восновном будет определяться колебательной составляющей. Это будет область колебательных процессов. В области II, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов.

Устойчивость соединения звеньев

Последовательное соединение

Характеристическое уравнение Q (p) = 0 Þ Q ₁(p)× Q ₂(p) = 0 Þ

Q ₁(p) = 0, Q ₂(p) =0.

Понятно, что корни характеристического уравнения системы – есть корни характеристических уравнений отдельных звеньев соединения. Следовательно, условием устойчивости последовательного соединения является устойчивость всех входящих в него звеньев.

Параллельное соединение

Характеристическое уравнение Q (p) = 0 Þ Q ₁(p)× Q ₂(p) = 0 Þ
Q ₁(p) = 0, Q ₂(p) =0.

Следовательно, условием устойчивости параллельного соединения является устойчивость всех входящих в него звеньев.

Соединение с обратной связью

Характеристическое уравнение Q (p)=0 Þ P ₁(p)× P ₂(p) + Q ₁(p)× Q ₂(p) = 0.

В этом случае возможны различные варианты, например, оба звена устойчивы, а система в целом неустойчива или какое-либо звено неустойчиво, а система устойчива.

Пример. Условия устойчивости движения колонны манипулятора

Рассматриваются условия устойчивости движения вращательной степени подвижности манипулятора (рис. 2.38). Отметим, что та же проблема возникает при исследовании поворотных платформ для градуировки датчиков угловых скоростей или центрифуг для градуировки акселерометров.

Рис. 2.38. К исследованию устойчивости движения колонны манипулятора

Математическая модель

· J j” = M – баланс моментов сил;

· M = c_м i – момент двигателя;

· Li’ + Ri = u – c_е j’ — баланс напряжений в якорной цепи двигателя;

· u = k ₁ u _у – напряжение в якорной цепи;

· u _у = k ₂ (j*–j) – управляющее напряжение.

Структурная схема

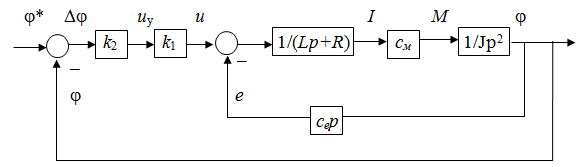
Рис. 2.39. Структурная схема системы

Q (p) = p [ Jp (Lp+R) + c_ec_м ] + k₁k₂c_м = JLp³+JRp²+ c_ec_мp+ k ₁ k ₂ c_{м .}

a ₀ = JLp ³; a ₁ = JRp ²; a ₂ = c_ec _м p; a ₃ = k ₁ k ₂ c _м.

Условия устойчивости: k ₁, k ₂ >0; JLk ₁ k ₂ c_м < JRc_ec_м Þ k ₁ k ₂ < Rc_e /L.

Поиск по сайту: