Алгебраические уравнения

Любое уравнение P (x)=0, где P (x) - это многочлен, отличный от нулевого, называется алгебраическим уравнением (полиномом) относительно переменной x. Всякое алгебраическое уравнение относительно x можно записать в виде

a ₀ x ⁿ+ a ₁ x ^n–1+…+ a _n–1 x + a _n=0,

где a ₀≠0, n ³1 и a_i – коэффициенты алгебраического уравнения n –й степени. Например, линейное уравнение - это алгебраическое уравнение первой степени, квадратное – второй, кубическое – третьей и так далее.

Решить алгебраическое уравнение в MathCAD можно при помощи двух встроенных функций:

root(F(x), x) – возвращает с заданной точностью значение переменной x, при котором выражение F(x) равно нулю, функция реализует вычисление итерационным методом, и перед ее применением необходимо задать начальное значение переменной x, принадлежащее интервалу изоляции корня;

polyroots(v) – возвращает вектор всех корней (как вещественных, так и комплексных) полинома n –й степени, коэффициенты которого хранятся в массиве v, длиной n +1.

Решим несколько алгебраических уравнений.

ЗАДАЧА 5.1. Найти корни полинома 2 x ⁴–8 x ³+8 x² –1=0.

Решим это уравнение при помощи функции polyroots(v). Массив коэффициентов, используемый в этой функции, определим как вектор столбец из пяти элементов (способы задания массива коэффициентов см. в задачах 5.2 и 5.3). Обратите внимание, что в уравнении отсутствует переменная x в первой степени. Это означает, что соответствующий коэффициент равен нулю.

Полностью решение задачи приведено на рис. 7. 13.1.

Рис. 7. 13.1. Вычисление корней полинома

Найдем графическое решение заданного уравнения. Для этого создадим функцию F (x), определив полином как сумму произведений коэффициентов на x в соответствующей степени, и построим ее график. Точки пересечения графика с осью абсцисс и будут корнями уравнения. На рис. 7.13.2 видно, что графическое решение совпадает с аналитическим.

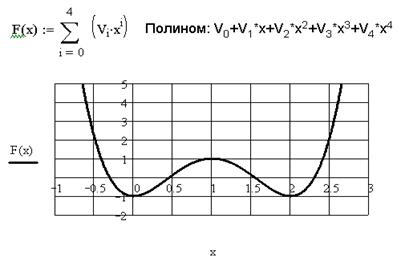
Рис. 7.13. 2. Графическое решение уравнения

ЗАДАЧА 7.13.1. Найти решение уравнения x ³+0.4 x² +0.6 x –1.6=0.

Решение этой задачи аналогичной предыдущей. Разница заключается в способе задания массива коэффициентов для дальнейшего использования в функции polyroots(v). Остановимся на этом вопросе подробнее.

Итак, определить вектор коэффициентов многочлена можно при помощи символьной операции Polynomial Coefficient, вызываемой из меню Symbolics. При этом многочлен должен быть введен в рабочий лист, и одна из переменных выделена.

Далее полученный вектор необходимо присвоить какой либо переменной и найти решение, вызвав функцию вычисления корней полинома. Результаты аналитического и графического решений приведены на рис. 7.13.3.

ЗАДАЧА 7.13.2. Найти решение уравнения y (x)=0, если y (x)= x ⁴–18 x² +6.

В этой задаче, как и в задаче 7.13. 1, акцент делается на метод определения коэффициентов полинома. На этот раз воспользуемся операцией Coeffs, которая находится на панели инструментов Symbolic. На рис. 7.13.4.видно, что эта операция содержит два поля ввода. Слева вводят многочлен, справа - неизвестную переменную, от которой он зависит.

На рис. 7.13.3.приведено численное и графическое решение задачи.

Рис. 7.13.3. Численное и графическое решение полинома

Рис. 7.13.4. Вызов операции определения коэффициентов полинома

Рис. 7.13.5. Решение алгебраического уравнения

ЗАДАЧА 7.13.4 Найти решение уравнения y (x)=0, если y (x)= x ⁵– x³ +1.

Решим эту задачу при помощи функции root(F(x), x). Для этого выполним следующую последовательность действий:

· введем функцию у (x) в рабочий лист;

· определим интервал изоляции корня, для чего выполним построение графика функции у (x);

· присвоим переменной x значение одного из пределов интервала изоляции, задав тем самым начальное значение;

· запишем функцию root(y(x),x) и вычислим корень уравнения.

На рис. 7.13.6. приведен ход решения задачи.

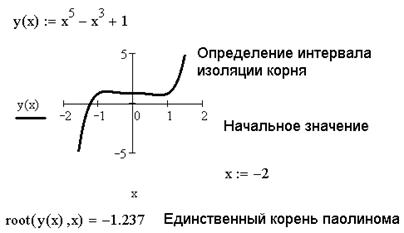
Рис. 7.13.6. Вычисление действительного корня полинома

На рис. 7.13.7. показано вычисление всех корней уравнения при помощи функции polyroots(v). Заметим, среди них есть и мнимые корни.

Рис7.13.7. Вычисление корней полинома

Далее будет рассмотрено применение функции root(F(x), x) для решения неалгебраических уравнений.

Поиск по сайту: