 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема 2 (интегральная теорема Коши для системы контуров)
Пусть полная граница  многосвязной области
многосвязной области  состоит из нескольких замкнутых жордановых спрямляемых кривых: внешней
состоит из нескольких замкнутых жордановых спрямляемых кривых: внешней  и внутренних
и внутренних  , причем таких, что для любого
, причем таких, что для любого  кривые
кривые  при
при  лежат во внешности
лежат во внешности 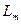 . Предположим, что обход полной границы
. Предположим, что обход полной границы  области
области  происходит в положительном направлении, то есть внешняя кривая обходится в положительном, а внутренние
происходит в положительном направлении, то есть внешняя кривая обходится в положительном, а внутренние  - в отрицательном направлении. Далее, пусть функция
- в отрицательном направлении. Далее, пусть функция  аналитична в такой области
аналитична в такой области  и непрерывна в замкнутой области
и непрерывна в замкнутой области 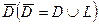 . Тогда имеет место равенство
. Тогда имеет место равенство
 ,
,
то есть
 . (4.4.4)
. (4.4.4)
Доказательство. Проведем гладкие, попарно непересекающиеся, целиком лежащие в  , кривые
, кривые  ,соединяющие кривую
,соединяющие кривую  с кривыми
с кривыми  и т. д. Тогда область, ограниченная кривыми
и т. д. Тогда область, ограниченная кривыми  и кривыми
и кривыми  , проходимыми дважды в противоположных направлениях, оказывается односвязной. В силу теоремы 1 интеграл по границе этой области равен нулю. Но интегралы по вспомогательным кривым
, проходимыми дважды в противоположных направлениях, оказывается односвязной. В силу теоремы 1 интеграл по границе этой области равен нулю. Но интегралы по вспомогательным кривым  проходятся дважды в противоположных направлениях и при суммировании интегралов выпадают. Поэтому приходим к равенству (4.4.4). Теорема доказана.
проходятся дважды в противоположных направлениях и при суммировании интегралов выпадают. Поэтому приходим к равенству (4.4.4). Теорема доказана.
Интегральная формула Коши
Пусть  − замкнутый жорданов спрямляемый контур. Обозначим через
− замкнутый жорданов спрямляемый контур. Обозначим через  конечную часть плоскости, ограниченную
конечную часть плоскости, ограниченную  , а через
, а через  − бесконечную часть плоскости, состоящую из точек, расположенных вне
− бесконечную часть плоскости, состоящую из точек, расположенных вне  . Контур
. Контур  не будем причислять ни к
не будем причислять ни к  , ни к
, ни к  . Область, состоящую из
. Область, состоящую из  и из точек линии
и из точек линии  , как обычно, будем обозначать через
, как обычно, будем обозначать через  , а область, состоящую из
, а область, состоящую из  и из точек линии
и из точек линии  , − через
, − через  . В качестве положительного направления на
. В качестве положительного направления на  выберем то, которое оставляет область
выберем то, которое оставляет область  слева.
слева.
Для дальнейших целей докажем следующую теорему:
Теорема 1. Пусть  − непрерывная функция на спрямляемой жордановой замкнутой или разомкнутой кривой
− непрерывная функция на спрямляемой жордановой замкнутой или разомкнутой кривой  . Функция
. Функция  , представленная интегралом типа Коши
, представленная интегралом типа Коши
 (4.5.1)
(4.5.1)
является аналитической функцией на комплексной плоскости 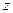 всюду вне кривой
всюду вне кривой  . Эта функция в точках
. Эта функция в точках 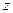 , не лежащих на
, не лежащих на  , имеет производные всех порядков, и для них справедливы формулы
, имеет производные всех порядков, и для них справедливы формулы

 (4.5.2)
(4.5.2)
Доказательство. Ввиду того, что  при
при  как функция
как функция 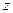 в каждой точке, не лежащей на
в каждой точке, не лежащей на  , имеет производные любого порядка
, имеет производные любого порядка
 , (4.5.3)
, (4.5.3)
а выражение  как функция
как функция  , для всех
, для всех 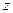 вне
вне  , непрерывна (и, следовательно, интеграл
, непрерывна (и, следовательно, интеграл  существует и является однозначной функцией
существует и является однозначной функцией 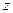 для любого
для любого  ), становится очевидным существование простых различных способов доказательства этой теоремы. Воспользуемся одним из них. Так как функция
), становится очевидным существование простых различных способов доказательства этой теоремы. Воспользуемся одним из них. Так как функция  при
при  как функция
как функция 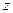 аналитична в каждой точке, не лежащей на
аналитична в каждой точке, не лежащей на  , то есть
, то есть  и операцию
и операцию  можно внести под знак интеграла в правой части (4.5.1), заключаем, что
можно внести под знак интеграла в правой части (4.5.1), заключаем, что  . Следовательно, функция
. Следовательно, функция  аналитична на комплексной плоскости
аналитична на комплексной плоскости 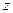 всюду вне кривой
всюду вне кривой  . Далее, в силу законности операции
. Далее, в силу законности операции
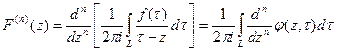 ,
,
для всех 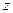 вне кривой
вне кривой  , с учетом (1.5.3) приходим еще к одному выводу: представленная интегралом типа Коши (4.5.1) функция
, с учетом (1.5.3) приходим еще к одному выводу: представленная интегралом типа Коши (4.5.1) функция  в точках
в точках 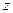 , не лежащих на
, не лежащих на  , имеет производные всех порядков, и для них справедливы формулы (4.5.2). Теорема доказана.
, имеет производные всех порядков, и для них справедливы формулы (4.5.2). Теорема доказана.
Приведем теперь следующие, хорошо известные формулы (в дальнейшем предполагается, что  - замкнутая спрямляемая кривая Жордана).
- замкнутая спрямляемая кривая Жордана).
I. Пусть  - функция, аналитическая в
- функция, аналитическая в  и непрерывная в
и непрерывная в  . Тогда
. Тогда

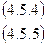
Формула (4.5.4) называется интегральной формулой Коши, а стоящий слева интеграл - интегралом Коши. Формула (4.5.5) – непосредственное следствие теоремы Коши (см. теорема 1 в параграфе 4.4), ибо в этом случае подынтегральная функция 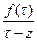 , рассматриваемая как функция от
, рассматриваемая как функция от  , аналитична в
, аналитична в  и непрерывна в
и непрерывна в  .
.
Для доказательства формулы (4.5.4) опишем из точки  , как из центра, окружность
, как из центра, окружность  настолько малого радиуса
настолько малого радиуса  , чтобы она принадлежала в
, чтобы она принадлежала в  . Учитывая аналитичность по
. Учитывая аналитичность по  функции
функции 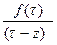 в области
в области  , получающейся из
, получающейся из  путем исключения точки
путем исключения точки 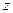 вместе с замкнутым кругом
вместе с замкнутым кругом  , и непрерывность ее вплоть до границы, в силу теоремы Коши для системы контуров (теорема 2 в параграфе 4.4) получаем
, и непрерывность ее вплоть до границы, в силу теоремы Коши для системы контуров (теорема 2 в параграфе 4.4) получаем
 (4.5.6)
(4.5.6)
где интегралы берутся в одном и том же направлении − в направлении против часовой стрелки. Из (4.5.6) следует:
а) доказательство формулы (4.5.4) сводится к доказательству
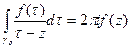
б) величина интеграла
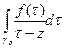
не изменяется при уменьшении радиуса окружности  , то есть
, то есть
 .
.
Стало быть, вместо доказательства формулы (4.5.4) достаточно установить справедливость равенства
 (4.5.7)
(4.5.7)
Справедлива запись
 ,
,
откуда на основании
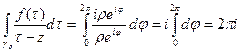
и очевидного равенства
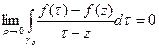
приходим к формуле (4.5.7), и тем самым – к формуле (4.5.4)
Очевидно, что формула
 ,
, 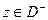
остается в силе и тогда, когда  представляет собой
представляет собой  - связную ограниченную область, контур
- связную ограниченную область, контур  которой состоит из замкнутых попарно непересекающихся жордановых спрямляемых кривых
которой состоит из замкнутых попарно непересекающихся жордановых спрямляемых кривых  . В частности, когда конечная область
. В частности, когда конечная область  с границей
с границей  содержит внутри себя
содержит внутри себя  , то можно написать
, то можно написать
 ,
, 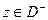 (4.5.8)
(4.5.8)
Следствие 1. Пусть в частном случае  − окружность с центром
− окружность с центром  .
.
Если  − радиус окружности, то уравнение окружности можно представить в виде
− радиус окружности, то уравнение окружности можно представить в виде 
 .
.
Следовательно,
 .
.
Под арифметическим средним функции  на окружности
на окружности  понимают
понимают
 ,
,
где  .
.
Иначе говоря, значение аналитической функции  в любой точке
в любой точке  области аналитичности равно арифметическому среднему ее значений на любой окружности с центром
области аналитичности равно арифметическому среднему ее значений на любой окружности с центром  , принадлежащей той же области.
, принадлежащей той же области.
Следствие 2. Пусть  аналитична и отлична от нуля в круге
аналитична и отлична от нуля в круге  . Можно показать, что геометрическое среднее модуля
. Можно показать, что геометрическое среднее модуля  на окружности
на окружности  есть
есть
 .
.
[Функция  аналитична в круге
аналитична в круге  .]
.]
Следствие 3. Если функция  аналитична в области
аналитична в области  и непрерывна в
и непрерывна в  , то она имеет в области
, то она имеет в области  производные всех порядков, и для них справедливы формулы
производные всех порядков, и для них справедливы формулы

 (4.5.8)
(4.5.8)
Здесь 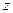 - произвольная точка области
- произвольная точка области  .
.
Действительно, в силу интегральной формулы Коши имеет место представление

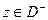 ,
,
и данное утверждение сразу следует из теоремы 1.
Из формулы (4.5.8) вытекают важные неравенства Коши. Обозначим через  максимум модуля функции
максимум модуля функции  в области
в области  , через
, через  - расстояние от точки
- расстояние от точки 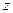 до границы
до границы  и через
и через  - длину жордановой спрямляемой кривой
- длину жордановой спрямляемой кривой  .
.
Имеем из (4.5.8):

Если, в частности,  - окружность с центром
- окружность с центром  и радиусом
и радиусом  , то
, то
 (4.5.9)
(4.5.9)
Это и есть неравенства Коши.
Следствие 4. Производная аналитической функции сама является аналитической функцией.
Действительно,  обладает производной
обладает производной  всюду в области
всюду в области  .
.
Итак, если функция  является аналитической функцией в области
является аналитической функцией в области  , то в этой области функция
, то в этой области функция  обладает непрерывными производными всех порядков. Это свойство аналитической функции комплексной переменной существенным образом отличает ее от функции действительной переменной, имеющей непрерывную первую производную в некоторой области. В последнем случае из существования первой производной, вообще говоря, не следует существование высших производных.
обладает непрерывными производными всех порядков. Это свойство аналитической функции комплексной переменной существенным образом отличает ее от функции действительной переменной, имеющей непрерывную первую производную в некоторой области. В последнем случае из существования первой производной, вообще говоря, не следует существование высших производных.
Следствие 5. Действительная и мнимая части аналитической функции обладают дифференцируемыми частными производными всех порядков.
Пусть 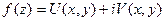 . Так как функция
. Так как функция  сама аналитична в области
сама аналитична в области  , то
, то  и
и  имеют частные производные первого порядка
имеют частные производные первого порядка  , причем в силу условия Коши-Римана
, причем в силу условия Коши-Римана
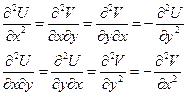
Тем самым доказаны существование производных второго порядка у функций 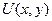 и
и  и гармоничность этих функций в области
и гармоничность этих функций в области  . Повторением этого рассуждения убеждаемся в том, что функции
. Повторением этого рассуждения убеждаемся в том, что функции 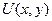 и
и  имеют производные всех порядков в области
имеют производные всех порядков в области  аналитичности функции
аналитичности функции  .
.
Действительная и мнимая части аналитической в области  функции
функции  называются сопряженными гармоническими функциями.
называются сопряженными гармоническими функциями.
Пусть 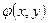 - какая-либо функция, гармоническая (однозначная) в данной односвязной области
- какая-либо функция, гармоническая (однозначная) в данной односвязной области  . Требуется найти функцию
. Требуется найти функцию 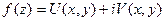 , аналитическую в этой области, действительная часть которой совпадает с
, аналитическую в этой области, действительная часть которой совпадает с 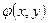 :
:  . Для отыскания мнимой части функции
. Для отыскания мнимой части функции  имеем два уравнения Коши- Римана:
имеем два уравнения Коши- Римана:
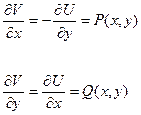
Функции  и
и  непрерывны в области
непрерывны в области  и обладают в ней непрерывными частными производными первого порядка. При этом выполняется условие
и обладают в ней непрерывными частными производными первого порядка. При этом выполняется условие
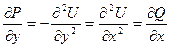 ,
,
в силу которого криволинейный интеграл
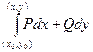
не зависит от вида пути, соединяющего точки  и
и  области
области  и, следовательно, представляет однозначную функцию
и, следовательно, представляет однозначную функцию  точки
точки  , т. е.
, т. е.
 .
.
Эта функция имеет те же частные производные, что и искомая функция  :
:
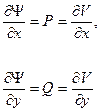
поэтому  может отличаться от
может отличаться от  только на постоянное слагаемое:
только на постоянное слагаемое:
 .
.
Здесь  - действительное число.
- действительное число.
Вычисляя  по этой формуле, будем иметь две дифференцируемые в области
по этой формуле, будем иметь две дифференцируемые в области  функции
функции
 ,
,
связанные уравнениями Коши-Римана
 ,
,  .
.
Отсюда следует, что функция
 , (4.5.10)
, (4.5.10)
где  , является аналитической функцией в односвязной области
, является аналитической функцией в односвязной области  .
.
Итак, искомая аналитическая функция  в односвязной области
в односвязной области  построена по формуле (4.5.10).
построена по формуле (4.5.10).
Аналогичное рассуждение показало бы, что функцию  можно было бы построить и по заданной ее мнимой части
можно было бы построить и по заданной ее мнимой части  .
.
Опираясь на следствие, докажем сейчас так называемую теорему Морера, до некоторой степени обратную к теореме Коши.
Теорема 2. Пусть функция  является непрерывной в односвязной области
является непрерывной в односвязной области  и интеграл от
и интеграл от  по замкнутому спрямляемому контуру, целиком принадлежащему
по замкнутому спрямляемому контуру, целиком принадлежащему  , равен нулю. Тогда
, равен нулю. Тогда  является аналитической функцией в области
является аналитической функцией в области  .
.
Доказательство. Возьмем какую-либо фиксированную точку 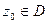 и рассмотрим интеграл
и рассмотрим интеграл
 .
.
Из условий теоремы следует, что он не зависит от пути интегрирования и поэтому является однозначной функцией от 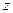 . В параграфе 4.4 показано, что функция
. В параграфе 4.4 показано, что функция  имеет в области
имеет в области  производную, равную
производную, равную  . Следовательно, функция
. Следовательно, функция  является аналитической функцией в области
является аналитической функцией в области  . По следствию 4 функция
. По следствию 4 функция  , равная производной функции
, равная производной функции  , тоже аналитична в области
, тоже аналитична в области  .
.
Эта теорема показывает, что при определении понятия аналитической функции можно исходить не из требования дифференцируемости, а из существования неопределенного интеграла.
Теорема 3 (теорема Лиувилля). Пусть на всей комплексной плоскости функция  является аналитической, а ее модуль равномерно ограничен. Тогда это функция
является аналитической, а ее модуль равномерно ограничен. Тогда это функция  тождественно равна постоянной.
тождественно равна постоянной.
Доказательство. По условию теоремы существует такая константа  , что
, что  независимо от
независимо от  . Поэтому согласно неравенству Коши (4.5.9)
. Поэтому согласно неравенству Коши (4.5.9)
 .
.
Так как радиус  можно выбрать сколь угодно большим, а
можно выбрать сколь угодно большим, а 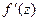 не зависит от
не зависит от  , то
, то  . В силу произвольности выбора точки
. В силу произвольности выбора точки 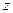 заключаем, что
заключаем, что  на всей комплексной плоскости. Отсюда следует, что
на всей комплексной плоскости. Отсюда следует, что  .
.
Поиск по сайту: