 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема Коши
Понятие неопределенного интеграла имеет смысл только для аналитических функций. Пусть функция 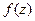 аналитична в области
аналитична в области  и пусть в этой области определена аналитическая функция
и пусть в этой области определена аналитическая функция  , причем
, причем  . Тогда функцию
. Тогда функцию  будем называть неопределенным интегралом (или первообразной) функции
будем называть неопределенным интегралом (или первообразной) функции 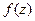 . Для неопределенного интеграла будем использовать обозначение
. Для неопределенного интеграла будем использовать обозначение
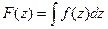
Понятие неопределенного интеграла от аналитической функции имеет смысл главным образом потому, что определенный интеграл от аналитической функции не зависит от пути интегрирования, и определенный интеграл можно выразить через определенный интеграл с переменным верхним пределом. Именно, справедлива следующая фундаментальная теорема, носящая название теоремы Коши:
Основная теорема Коши. П усть  - конечная односвязная область и пусть функция
- конечная односвязная область и пусть функция 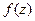 однозначна и аналитична в этой области. Если
однозначна и аналитична в этой области. Если  - спрямляемая кривая с началом в точке
- спрямляемая кривая с началом в точке 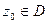 и концом в произвольной точке
и концом в произвольной точке 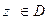 , лежащая в области
, лежащая в области  , то интеграл
, то интеграл
 (4.4.1)
(4.4.1)
не зависит от выбора пути интегрирования, а зависит исключительно от начальной и конечной точки этого пути. Считая точку  фиксированной, можно рассматривать интеграл (4.4.1) как однозначную функцию верхнего предела
фиксированной, можно рассматривать интеграл (4.4.1) как однозначную функцию верхнего предела 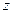 . Эта функция аналитична в области
. Эта функция аналитична в области  , причем ее производная равна
, причем ее производная равна 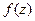 .
.
Эта теорема при дополнительных ограничениях, когда 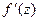 непрерывна в области
непрерывна в области  , а
, а  есть жорданова кусочно-гладкая кривая, принадлежащая области
есть жорданова кусочно-гладкая кривая, принадлежащая области  и соединяющая точку
и соединяющая точку  с произвольной точкой
с произвольной точкой 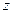 области
области  , легко доказывается, опираясь на теоремы о криволинейных интегралах второго типа от действительных переменных. Однако в данной теореме предполагается только существование
, легко доказывается, опираясь на теоремы о криволинейных интегралах второго типа от действительных переменных. Однако в данной теореме предполагается только существование 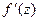 во всех точках области
во всех точках области  , а
, а  является спрямляемой кривой и поэтому, доказательство наиболее существенной части основной теоремы Коши опирается на следующее утверждение:
является спрямляемой кривой и поэтому, доказательство наиболее существенной части основной теоремы Коши опирается на следующее утверждение:
Интегральная теорема Коши. Если функция 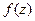 однозначна и аналитична в конечной односвязной области
однозначна и аналитична в конечной односвязной области  , то ее интеграл вдоль любого замкнутого спрямляемого контура
, то ее интеграл вдоль любого замкнутого спрямляемого контура  , лежащего в области
, лежащего в области  , равен нулю:
, равен нулю:
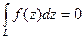 .
.
Доказательство этой теоремы, не предполагающее непрерывности 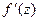 , впервые было дано Э. Гурса и затем упрощено А. Прингхеймом; оно имеется во многих руководствах по теории аналитических функций.
, впервые было дано Э. Гурса и затем упрощено А. Прингхеймом; оно имеется во многих руководствах по теории аналитических функций.
Теперь, опираясь на интегральную теорему Коши, перейдем к доказательству основной теоремы Коши.
Из интегральной теоремы Коши следует, что интегралы от функции 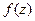 , однозначной и аналитической в односвязной области
, однозначной и аналитической в односвязной области  , вдоль любых двух спрямляемых кривых
, вдоль любых двух спрямляемых кривых 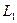 и
и 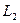 , лежащих в области
, лежащих в области  , с общим началом в точке
, с общим началом в точке 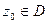 и концом в произвольной точке
и концом в произвольной точке 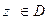 имеют равные значения. Действительно, спрямляемая кривая
имеют равные значения. Действительно, спрямляемая кривая  является замкнутой и, следовательно,
является замкнутой и, следовательно,
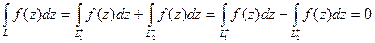 ,
,
откуда
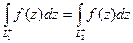
Итак, значение интеграла от аналитической функции 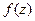 не зависит от той кривой, по которой производится интегрирование (от пути интегрирования), а зависит исключительно от начальной и конечной точек этой кривой. По этой причине для обозначения интеграла можно использовать символ
не зависит от той кривой, по которой производится интегрирование (от пути интегрирования), а зависит исключительно от начальной и конечной точек этой кривой. По этой причине для обозначения интеграла можно использовать символ
 ,
,
опуская указание на путь интегрирования и отмечая только начальную и конечную точки 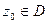 и
и 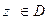 .
.
Так как 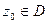 фиксированная, то интеграл этот представляет собой однозначную функцию от
фиксированная, то интеграл этот представляет собой однозначную функцию от 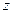
 .
.
Остается доказать, что функция  является аналитической функцией в области
является аналитической функцией в области  , причем ее производная равна подынтегральной функции
, причем ее производная равна подынтегральной функции  .
.
Пользуясь непрерывностью функции 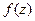 (непрерывность функции
(непрерывность функции 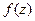 является следствием ее аналитичности), построим
является следствием ее аналитичности), построим  - окрестность произвольной точки
- окрестность произвольной точки 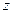 области
области  так, чтобы, во-первых, эта окрестность принадлежала области
так, чтобы, во-первых, эта окрестность принадлежала области  , а, во-вторых, чтобы для любой ее точки
, а, во-вторых, чтобы для любой ее точки  выполнялось неравенство
выполнялось неравенство
 .
.
Обозначим  какую-нибудь спрямляемую кривую, соединяющую
какую-нибудь спрямляемую кривую, соединяющую  и
и 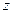 внутри области
внутри области  , и через
, и через  прямоугольный отрезок, соединяющий точку
прямоугольный отрезок, соединяющий точку 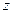 с произвольной точкой
с произвольной точкой 
 -окрестности. При достаточно малом
-окрестности. При достаточно малом  любую спрямляемую кривую, соединяющую точку
любую спрямляемую кривую, соединяющую точку 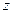 с точкой
с точкой  , можно считать прямолинейным отрезком. Точка
, можно считать прямолинейным отрезком. Точка  может находиться и на
может находиться и на  .
.
Стало быть, для всех точек  , то есть для всех точек
, то есть для всех точек  , для которых
, для которых  , где
, где  - длина прямолинейного отрезка
- длина прямолинейного отрезка  , а
, а  - радиус окружности, в силу непрерывности функции
- радиус окружности, в силу непрерывности функции  в точке
в точке 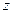 , выполняется соотношение
, выполняется соотношение
 (4.4.2)
(4.4.2)
где  при
при  и, следовательно, при
и, следовательно, при  .
.
Для отношения  в силу формулы (4.3.3) имеем
в силу формулы (4.3.3) имеем
 (4.4.3)
(4.4.3)
В дальнейшем для доказательства  достаточно потребовать только лишь непрерывность функции
достаточно потребовать только лишь непрерывность функции 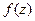 в
в  - окрестности и выполнение неравенства
- окрестности и выполнение неравенства  для любой ее точки
для любой ее точки  .
.
Подставляя (4.4.2) в (4.4.3) и замечая, что  , с учетом формулы (4.3.6), находим
, с учетом формулы (4.3.6), находим
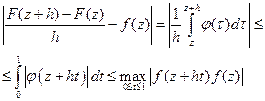
Отсюда ввиду того, что  при
при  получаем
получаем
 .
.
Основная теорема Коши доказана.
Следствие 1. Если функция 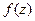 аналитична в односвязной области
аналитична в односвязной области  , то ее неопределенный интеграл может быть представлен так:
, то ее неопределенный интеграл может быть представлен так:

 ,
,
где  - произвольная комплексная постоянная.
- произвольная комплексная постоянная.
Следствие 2. Если  − произвольная первообразная аналитической функции
− произвольная первообразная аналитической функции 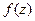 , то
, то
 ,
,
откуда при  , где
, где  − фиксированная точка, получаем
− фиксированная точка, получаем
 .
.
Эту формулу называют формулой Ньютона-Лейбница.
Замечание. В некоторых книгах интегральная теорема Коши формулируется так:
Если функция 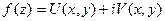 аналитична в ограниченной области
аналитична в ограниченной области  с кусочно-гладким жордановым контуром
с кусочно-гладким жордановым контуром  и функции
и функции 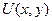 и
и  непрерывны вместе со своими частными производными первого порядка в
непрерывны вместе со своими частными производными первого порядка в 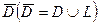 , то
, то
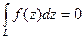
Доказательство. Очевидно, все условия Утверждения в §4.3 соблюдены и, следовательно, имеет место формула Римана-Грина
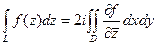
Для аналитических функций двойной интеграл исчезает, так как  .
.
Теорема доказана.
В интегральной теореме Коши речь идет об интеграле по контуру  , целиком лежащем у внутри области аналитичности функции, между тем, часто приходится рассматривать интегралы вдоль кривых, на которых функция, оставаясь непрерывной, перестает быть аналитичной. Оказывается, интегральная теорема Коши остается в силе и для этого случая:
, целиком лежащем у внутри области аналитичности функции, между тем, часто приходится рассматривать интегралы вдоль кривых, на которых функция, оставаясь непрерывной, перестает быть аналитичной. Оказывается, интегральная теорема Коши остается в силе и для этого случая:
Теорема 1(вторая формулировка теоремы Коши). Если функция 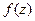 аналитична в области
аналитична в области  , ограниченной жордановой спрямляемой кривой
, ограниченной жордановой спрямляемой кривой  , и непрерывна в
, и непрерывна в  , то интеграл от функции
, то интеграл от функции 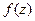 по
по  равен нулю:
равен нулю:
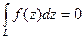
Для справедливости теоремы 1 существенную роль играет предположение об односвязности области  .
.
Для многосвязных областей имеет место следующий вариант этой теоремы:
Поиск по сайту: