 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Моделирование в разработке и принятии эффективного управленческого решения
В системе управления деятельностью организации чрезвычайно важным моментом, определяющим в конечном счете результативность функционирования системы в целом, является разработка и принятие управленческого решения. Именно на этом уровне управления осуществляется соединение основных составляющих производства – средств труда, предметов труда и самого труда, устанавливается и поддерживается необходимая пропорциональность между ними, что обеспечивает рациональность использования имеющихся у организации ресурсов. Правильно сочетать эти элементы производства как в рамках организации в целом, так и по его отдельным подразделениям – важнейшая управленческая задача. Рациональность ее решения в известной мере определяется эффективностью использования специального инструментария – моделей, методов и приемов.
Особенностью решения задач управления является необходимость учета множества переменных величин, характеризующих постоянно изменяющуюся внешнюю и внутреннюю среду. А так как число сочетаний этих величин в течение определенного времени (планового, учетного, отчетного и т.п. периодов) может быть достаточно большим, то возможно существование значительного числа вариантов управленческих решений. Отсюда большая размерность решаемых задач. И, тем не менее, необходимо получить оптимальное или близкое к нему решение. В этих условиях простой перебор и сравнение всех возможных вариантов решения конкретной управленческой задачи нереальны из-за большой трудоемкости вычислений. Поэтому требуются специальные методы, позволяющие в приемлемые сроки с достаточной степенью обоснованности с учетом особенностей конкретного объекта выйти на искомое решение.
Спектр применяемых в управлении специальных методов и приемов чрезвычайно велик, поэтому не представляется возможным в рамках ограниченного объема данного пособия описать все или хотя бы большинство из них.
В управленческой деятельности существенное место занимают решения по управлению инновационной деятельностью, поскольку она оказывает существенное влияние на перспективы развития организации, ее конкурентоспособность и т.п. Управление инновационной деятельностью организации характеризуется большим объемом и разнообразием решаемых задач:
· выбор инновационных объектов;
· разработка инновационных проектов, пространственная и временная регламентация их реализации;
· расчет потребных ресурсов;
· поиск источников финансирования инновационных проектов;
· обеспечение мониторинга реализации инновационных проектов;
· принятие соответствующих мер по недопущению срывов в инновационной деятельности и т.п.
· выявление отклонений в выполнении запланированных работ и принятие мер по недопущению их срывов и т.п.
Далее в таблице 3.1 сгруппированы методы, подходы и приемы с описанием их сущности, сфер и особенностей применения при разработке и принятии управленческих решений, в том числе и в области инновационного менеджмента.
Все решаемые задачи управления взаимосвязаны. Эта взаимосвязь обусловлена, прежде всего, единым ресурсным потенциалом, имеющимся у организации. Поэтому при решении любой локальной задачи или их комплекса необходима временная, ресурсная, пространственная увязка. Выполнить такую работу можно на базе моделирования.
Модель – это условный образ объекта управления (системы или процесса), для которых разрабатывается управленческое решение, представляющий собой взаимосвязь элементов системы или объекта, являющихся основными с точки зрения решаемой задачи.
Модель – не эквивалент конкретного объекта, для которого решается проблема или задача, это только его образ. В модели присутствуют не все элементы объекта, а только наиболее существенные с точки зрения решаемой задачи (проблемы). Несущественные признаки (элементы) отбрасываются, существенные же используются для описания объекта на базе установленных между ними взаимосвязей (соотношений). Условный образ моделируемого объекта гомоморфен (подобен) реальному объекту, а модель – изоморфна (соответственна) образу: каждому элементу условного образа соответствует элемент реального объекта, но не наоборот; каждому соотношению элементов условного образа соответствует соотношение элементов в реальном объекте, но не наоборот. Пренебрежение малозначащими для решения конкретной проблемы (задачи) элементами огрубляет разрабатываемую модель, при этом степень огрубления должна быть допустимой и не искажать сущности отражаемого объекта или процесса.
В зависимости от моделируемого объекта или процесса, решаемой задачи, цели управленческого решения, от используемого инструментария, организационно-правовой формы организации, от вида ее деятельности, от способа разработки модели и т.д. все разрабатываемые и используемые в системе управления модели могут быть сгруппированы по различным классификационным признакам.
Таблица 3.1
Характеристика и области применения различных методов разработки и принятия управленческих решений в менеджменте организации
| № п/п | Название метода | Сущность метода | Сфера применения | Преимущества | Недостатки |
| Деревья решений | Принятие статистических решений при выборе одного из альтернативных вариантов и формировании оптимальной стратегии | · Анализ эффективности виртуального проекта · Управление проектом | Решения, принимаемые в каждый момент времени, в большой степени зависят от принятых ранее решений и в свою очередь определяют сценарии дальнейшего развития ситуации | Применим, если проект имеет обозримое или разумное число вариантов развития | |
| Метод аналогий или консервативных прогнозов | Исследование накопленного опыта по проектам-аналогам с целью расчета вероятностей возникновения потерь | Оценка часто повторяющихся ситуаций, решений, проектов | Наличие данных | Применим только для уже имевших ранее место проектов и решений | |
| Планирование эксперимента | Построение матриц планирования эксперимента для количественной оценки воздействия составляющих проекта на его эффективность, построение регрессионной модели проекта для оценки взаимосвязей элементов | · Установление взаимосвязей между элементами проекта · Управление проектом · Количественный анализ рисковости | · Возможность изучения взаимодействия переменных и их комплексного влияния на реализацию проекта · Возможность оценки влияния влияние на проект различных управленческих решений с точки зрения их эффективности | Исключает учет корреляции факторов | |
| Метод имитационного моделирования | Расчет большого числа случайных вариантов (сценариев) реализации проекта Распределение вероятностей интегрального показателя эффективности проекта | Количественная оценка рисковости проекта в целом | · Широкие возможности использования в условиях неопределённости · Практически неограниченное количество случайных сценариев при гарантированной вероятности надежности результатов моделирования · Возможность удачного сочетания с различными экономико-статистическими методами, а также с теорией игр и другими методами исследования операций | · Позволяет получать только интегральные оценки эффективности и рисковости проекта · Не позволяет оценить воздействие на проект его отдельных переменных | |
| Продолжение таблицы 3.1 | |||||
| Анализ чувствительности | Анализ поведения критериальных показателей проекта в результате изменения только одного рискового фактора (однофакторный анализ) | Количественный анализ | Хорошо иллюстрирует влияние отдельных исходных факторов на конечный результат проекта | · Управление проектом · Не учитывается взаимосвязь различных составляющих проекта · Изменение каждого фактора рассматривается изолированно | |
| Анализ сценариев | Анализ поведения критериальных показателей проекта в результате изменения спектра факторов, связанных с риском (многофакторный анализ) | Количественный анализ различных вариантов реализации проектов с учетом их рисковости | · Получение наглядной картины различных вариантов реализации проекта, что дает информацию о чувствительности и возможных отклонениях · Учет взаимосвязей между переменными | · Необходимость значительных качественных исследований моделей сценариев по отбору и переработке информации для создания нескольких сценариев · Неопределенность границ как самих сценариев, так и, в некоторой степени, оценок значений переменных каждого из сценариев · Сложность моделирования из-за роста числа сценариев и изменяемых переменных | |
| Метод ставки процента с поправкой на риск (метод корректировки нормы дисконта) | Определение возможного увеличения безрисковой ставки процента на величину надбавки за риск, т.е. возможность установления объективных показателей премии за риск | Учет влияния на функционирование организации дополнительных факторов внешней и внутренней среды при расчете эффективности принимаемых управленческих решений | Простота расчетов | · Не дает никакой информации о возможных отклонениях результатов по принятому решению. · Полученные результаты существенно зависят только от величины надбавки за риск | |
| Метод критических значений (анализ устойчивости) | Нахождение тех значений переменных (факторов), достижение которых соответствует критическому пределу эффективности проекта по соответствующему критерию | Мониторинг в процессе управления проектом в условиях риска и неопределенности | Возможность без дополнительных расчетов в условиях прогнозируемой динамики изменений оценить степень близости критериального показателя виртуального проекта к его критическому пределу | Дает лишь критическое значение исследуемого фактора |
В зависимости от моделируемого объекта или процесса, решаемой задачи, цели управленческого решения, от используемого инструментария, организационно-правовой формы организации, от вида ее деятельности, от способа разработки модели и т.д. все разрабатываемые и используемые в системе управления модели могут быть сгруппированы по различным классификационным признакам.
Модели, с помощью которых решаются задачи управления организацией (управления материальными, трудовыми, финансовыми и т.п. потоками), устанавливаются наиболее приемлемые для организации показатели ее хозяйственной, производственной, финансовой деятельности, т.е. экономические и финансовые показатели, относятся к классу экономико-математических. Их можно классифицировать следующим образом:
1) по объекту моделирования:
· модели системы;
· модели процесса, показывающие последовательность выполнения различных процессов либо работ.
2) по физической сущности:
· материальные (предметные, физические, технологические);
· нематериальные (математические, графические, имитационные, логические – модели, построенные на основе формальной или математической логики);
3) по форме представления (способу описания):
· вербальные, модели словесного описания.
Эти модели могут использоваться как на начальном этапе построения модели, так и самостоятельно. Моделями словесного описания можно считать, например, должностные инструкции, штатное расписание, деловые письма (модель некоторой ситуации), а также так называемые модели систем управления: бюрократическую модель Макса Вебера, неоклассическую модель, профессиональную модель и модель принятия решений Герберта Саймона;
· табличные;
· формульные (вероятностные, стоимостные, ресурсные, временные);
· графические, используемые для изучения организационной структуры управления, отображения взаимосвязей работ подразделений, распределения обязанностей и полномочий, изучения взаимосвязей и взаимозависимостей показателей и т.д. Эти модели в свою очередь можно классифицировать следующим образом:
v модели, выражающие структурные отношения и связи – без указания количественных характеристик (оргограммы);
v модели пространственные – описывающие моделируемый объект во времени и пространстве (хронограммы, топограммы);
v модели количественные – выражающие количественные соотношения (диаграммы, номограммы), в том числе классические графики;
v сетевые графы (одноцелевые, многоцелевые);
v математические (цифровые) модели;
Математические выражения зависимостей выходов от входов и параметров состояния принято называть математической моделью системы, если описание с достаточной полнотой отображает фактическое поведение системы, его особенности, важные для целей исследования или управления;
4) по характеру учета времени математические модели разделяются на:
· статические – модели системы, описывающие процессы ее функционирования в установившемся режиме. Типичными примерами для конкретного производства могут служить зависимости объема выпуска продукции, себестоимости и других экономических показателей от расхода основного сырья на входе в систему;
· динамические – описывающие изменения входов и параметров состояния системы в неустановившихся режимах [16].
5) по видам математического описания различают:
· детерминированные модели, построенные на основе изученных закономерностей процессов функционирования систем;
· стохастические модели, описывающие так называемые случайные, или стохастические процессы, результаты которых не всегда предсказуемы с достаточной точностью.
Стохастические процессы характеризуются функцией распределения вероятностей рассматриваемых событий. Если эта функция стабильна, т.е. не изменяется во времени, то стохастический процесс называется строго стационарным. Для стационарных процессов функция распределения вероятностей может быть установлена экспериментально. Это позволяет, используя модель теории вероятностей, построить стохастическую модель системы; свойства таких систем характеризуются не однозначными (функциональными), а корреляционными зависимостями, позволяющими установить наиболее вероятные значения выходов и других показателей функционирования системы.
Если стохастические процессы, влияющие на поведение системы, нестационарны, то ее поведение не всегда может быть описано математически, т.е. оказывается неформализуемым. Для количественной характеристики неформализуемых свойств, отражения взаимосвязей элементов таких систем, а также для прогноза результатов их функционирования используются, как правило, эвристические методы, в частности экспертные оценки.
6) по области применения (классам задач) выделяют модели:
· стратегического управления,
· текущего управления,
· оперативного управления.
7) по методам построения математические модели делятся на:
· статические, описывающие систему с неизвестной структурой и свойствами («черный ящик»), но с изученными статистическими зависимостями между параметрами элементов управляемой системы;
· параметрические модели, описывающие некоторое множество взаимосвязанных показателей, характеризующих тем или иным образом объект моделирования;
· модели теории игр;
Теория игр – это метод моделирования оценки воздействия принятого решения, например, на конкурентов. Игровые модели часто используются, когда требуется определить наиболее важные и требующие учета факторы в ситуации принятия решений в условиях конкурентной борьбы;
· модели теории очередей, используемые для определения оптимального числа каналов обслуживания по отношению к потребности в них. Модели очередей снабжают руководство инструментом определения оптимального числа каналов обслуживания, которые необходимо иметь, чтобы сбалансировать издержки в случаях чрезмерно малого или очень большого их количества;
· модели управления запасами, которые используются для определения времени размещения заказов на ресурсы и их количества, а также массы готовой продукции на складах. Цель построения таких моделей – сведение к минимуму отрицательных последствий накопления запасов, что увеличивает иммобилизацию оборотных средств, ведет к росту стоимости хранения запасов, повышает издержки, а, следовательно, снижает прибыльность;
· модели линейного программирования, применяемые для оптимального распределения ограниченных в т.ч. дефицитных ресурсов при наличии конкурирующих потребностей, т.е. при необходимости их использования для производства нескольких видов продукции, для осуществления различных видов деятельности и т.п.
· табличные (матричные);
· экономическо-математические (формульные, матричные, сетевые);
· сетевые модели, в составе которых можно выделить:
Ø циклограммы, представляющие собой открытый граф, включающий отдельные процедуры (элементы), реализация которых позволит достичь конечной цели. Порядок построения такой модели – от конечного к начальному событию, т.е. обратный ходу ее реализации;
Ø программно-целевые модели,позволяющие увязать ресурсы, необходимые для достижения цели, и цели через локальные программы, выполняемые в рамках общей программы;
Ø сетевые графы и т.п.
На практике также широко используют смешанные типы моделей, сочетающие в себе отдельные характерные признаки разных групп моделей. Так, например, параметрические модели соответственно содержат как математические уравнения, отражающие зависимость параметров объекта и субъекта, отдельных элементов субъекта, так и графические схемы, логически показывающие качественную сторону связей этих же параметров.
8) по характеру увязки элементов:
· аддитивные ( ),
),
например, прибыль = прибыль от реализации произведенной продукции (выполненных работ, оказанных услуг) + прибыль от прочей реализации + результаты внереализационной деятельности;
· мультипликативные (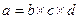 ),
),
например, объем выпуска продукции = численность персонала × количество отработанных дней одним работником × среднедневная производительность труда;
· кратные ( ),
),
например, фондоотдача = объем выпуска продукции (работ, услуг)/стоимость основных производственных фондов;
· смешанные ( ,
, 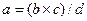 и др.),
и др.),
например, доход от реализации = цена единицы работы × объем реализованных работ + доход от прочей реализации и т.п.
Аддитивные, мультипликационные и кратные модели называют также базовыми факторными моделями. Работа с ними дает возможность расширять или сужать модель, маневрируя количеством используемых в модели показателей-факторов и находить наиболее высокую степень соответствия разработанной модели и реальной системы, которая обеспечит разработку и принятие наиболее обоснованного управленческого решения.
Показатели, используемые в факторных моделях, должны отвечать следующим требованиям: включаться не только в данную модель, но и в другие; являться самостоятельными показателями; иметь экономический смысл.
9) по целям исследования модели разделяются на: модели распределения ресурсов; модели упорядочения; модели управления процессами; модели поиска; модели выбора оптимального маршрута; модели решения состязательных задач и т.д.
В качестве элементов моделируемой системы могут выступать: процедуры, если объектом моделирования является какой-либо процесс; показатели или признаки, если объектом моделирования являются системы.
Элементы системы характеризуются количественно и качественно, при этом одни элементы имеют и количественную, и качественную характеристики, другие же – только качественную. Но для отображения зависимостей между элементами системы и для работы с моделью необходимы их количественные характеристики. Поэтому в случае, когда элементы системы характеризуются только качественными показателями, необходимо использовать специальные приемы или специальный аппарат для получения количественных показателей.
С позиций достижения определенных целей управления некоторые элементы системы являются существенными, определяющими ее поведение, другие – несущественными. Поэтому правомерно предположить, что отказ от учета последних при построении модели не приведет к серьезному рассогласованию результатов, рассчитанных на базе сформированной модели и полученных в реально функционирующей системе. Но при построении модели нельзя ограничиться только определяющими признаками, необходимо учитывать также и специфические, иначе модель потеряет связь с реальной системой и окажется непригодной для использования.
Отображение изучаемой системы как совокупности определяющих ее элементов, существенных с точки зрения поставленной цели, и взаимосвязей между ними гомоморфно (подобно) данной системе. Результатом этой работы является создание образа системы или какого-либо процесса. Этому образу строго соответствует построенная модель. В этом случае речь идет об адекватности (изоморфизме) образа системы и ее модели. Порядок построения модели представлен в таблице 3.2 [28].
Таблица 3.2
Схема построения модели
| Название этапа | Входная информация | Выходная информация, выполняемые процедуры |
| 1. Постановка задачи | 1.1. Экономическая теория 1.2. Результаты реальных явлений 1.3. Выводы, которые делает наука об организации и планировании процесса создания готового продукта, оказания услуги, выполнения работ | 1.1. Перечень величин, подлежащих определению и дающих объективную и исчерпывающую характеристику состояния объекта управления. 1.2. Условия, которые должны учитываться при определении значений величин, указанных выше. 1.3. Параметры, связывающие названные характеристики и условия. 1.4. Словесная четкая формулировка критерия или набора критериев оптимальности для оптимизационной задачи |
| 2. Формализованное описание | 2.1. Информация, полученная на выходе первого этапа | 2.1. Показатели, характеризующие объект управления, искомые величины, параметры процесса, факторы и условия, регламентирующие процесс производства (оказания услуг, выполнения работ).
2.2. Информация количественного характера, являющаяся исходной для формирования модели.
2.3. Зависимости моделируемого процесса, выраженные математическими символами в неявном виде, например: 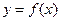 . .
|
| Продолжение таблицы 3.2 | ||
| 3. Формализация в общем виде | 3.1. Информация, полученная в результате реализации второго этапа | 3.1. Зависимости моделируемого процесса, выраженные в явном виде, например: 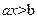 .
3.2. Рассматриваются вопросы снижения размерности задачи и упрощения формализованной записи. .
3.2. Рассматриваются вопросы снижения размерности задачи и упрощения формализованной записи.
|
| 4. Численное представление | 4.1. Информация третьего этапа 4.2. Конкретные данные моделируемого объекта или процесса | 4.1. Замена символов на конкретные
числовые данные, например:
 .
4.2. Проводится предварительная обработка данных для ввода в модель (агрегирование информации, определение законов распределения случайных величин, определение функциональных зависимостей динамических рядов, показателей). .
4.2. Проводится предварительная обработка данных для ввода в модель (агрегирование информации, определение законов распределения случайных величин, определение функциональных зависимостей динамических рядов, показателей).
|
После построения экономико-математической модели проводится ее экономико-математический анализ с целью выявления особенностей модели и выбора:
1) теории, в рамках которой может быть получено решение задачи;
2) группы или класса методов данной теории, наиболее пригодных для решения сформулированной задачи;
3) конкретного численного метода, который является наиболее целесообразным и эффективным для решения данной задачи на базе сформулированной экономико-математической модели, с учетом ее размерности и имеющейся вычислительной техники.
Если подходящий экономико-математический метод не выбран, необходимо упростить экономико-математическую модель. Для этого следует, задавшись трудновычисляемыми величинами или зависимостями, начать процесс построения экономико-математической модели с первого этапа.
Построение модели – очень сложный и трудоемкий процесс
как в методическом, так и в техническом (в части исполнения) плане.
Модель призвана заменить реально существующую систему,
поэтому она должна быть рабочей, действующей, что обеспечивается соблюдением ряда основных требований, сформулированных на базе основополагающих кибернетических принципов, теоретических разработок по моделированию систем, анализу и оценке опыта функционирования различных моделей при решении конкретных задач управления. К числу указанных требований относятся:
1) четкость постановки цели построения модели;
2) обязательность представления взаимосвязей и взаимозависимостей элементов модели в формализованном виде;
3) допустимая целесообразность степени упрощения при отображении реальной системы, в частности, экономической;
4) соответствие построенной модели поставленной цели;
5) обеспечение необходимой надежности модели.
Перечисленные требования нельзя рассматривать как самостоятельно действующие и изолированные друг от друга. Только комплексный их учет обеспечивает качество модели и обоснованность полученных с ее помощью результатов.
Четкость постановки цели занимает особое место в комплексе требований, предъявляемых к моделям. Поставленная цель определяет состав и количественную характеристику основных, определяющих систему элементов. Нечеткость постановки (размытость) цели исключает однозначный набор определяющих систему элементов, не позволяет выделить в комплексе взаимосвязей и взаимозависимостей этих элементов основные, обеспечивающие достижение данной цели. Следовательно, при нечеткой постановке цели будет иметь место не только высокая степень вероятности создания не работающей модели, не отвечающей поставленной цели, но и возможность принятия на ее основе ошибочных УР.
Обязательность представления взаимосвязей и взаимозависимостей в формализованном виде обеспечивает выполнение расчетов, связанных с выработкой расчетно обоснованного управленческого решения, принимаемого на основе установленных строгих математических зависимостей. Тем самым гарантируются объективность и реальность достижения результатов расчета, а, следовательно, и эффективность управленческого решения. Несоблюдение этого требования приведет к необходимости использования только логических умозаключений, носящих к тому же субъективный характер.
Целесообразность степени упрощения при отображении реальной экономической системы призвана обеспечить возможность работы с построенной моделью. Чрезмерное перенасыщение модели несущественными элементами, все более приближающими ее к реальной системе, может не только значительно усложнить процесс работы с моделью, но даже сделать эту работу невозможной. В то же время излишнее упрощение модели приведет к получению результатов, не свойственных реальной системе, так как существенные признаки и взаимосвязи элементов последней в сформированной модели будут потеряны.
Соответствие модели поставленной цели предопределяет выбор и включение в модель только основных, определяющих реальную экономическую систему элементов и установление между ними взаимозависимостей и взаимосвязей, обеспечивающих достижение поставленной цели и (или) оказывающих влияние на этот
процесс.
Обеспечение необходимой надежности модели призвано гарантировать экономическую безопасность работы с ней, достоверность получаемых результатов, разумный интервал рассогласования результатов моделирования с реальными показателями действующей экономической системы.
В последнее время все более широкое распространение получает использование имитационных моделей, особенностью построения которых является максимально возможная точность отображения моделируемой системы. Это предопределяется тем, что имитационные модели широко используются в исследованиях, при выявлении и установлении тенденций и закономерностей развития той или иной системы. Применительно к экономическим системам это может быть, например, решение задачи наилучшего использования производственной мощности, трудовых и материальных ресурсов, системы создания и поддержания на нормальном уровне заделов при диверсификации производства, разработки проектов освоения новых технологий и др., т. е. выработка различных стратегий функционирования организации, планирования и регулирования ее деятельности и т.п.
Для имитационного моделирования характерно широкое использование математического аппарата и компьютерной техники.
Поиск по сайту: