Спрямляемые кривые. Понятия комплексного интегрирования. Формула Римана-Грина

1. Спрямляемые кривые. Пусть где - действительный параметр, изменяющийся в пределах - непрерывная кривая. Каждому разбиению отрезка 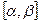на частичные отрезки соответствует разбиение кривой на частичные дуги с начальными точками 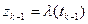и конечными точками ; при этом конечная точка каждой дуги (кроме последней) будет совпадать с начальной точкой следующей за ней дуги. Соединяя точки 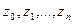по порядку отрезками прямых, получим ломаную , вписанную в кривую . Звенья этой ломаной суть хорды дуг 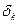. Очевидно, длина ломаной равна . Если эта величина, независимо от взятого разбиения, остается ограниченной:

,

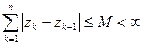то кривая называется спрямляемой, а верхняя грань указанных сумм называется длиной кривой.

Из определения длины спрямляемой кривой следует, что длина любой вписанной в кривую ломаной не превосходит длины кривой . Следовательно, длина спрямляемой кривой является пределом длин любой последовательности вписанных ломаных при условии, что максимальная длина сегментов, соответствующих разбиению отрезка 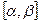, стремится к нулю. Частный класс спрямляемых кривых представляют гладкие кривые.

Непрерывная кривая называется гладкой, если среди параметрических уравнений кривой имеется хотя бы одно уравнение , такое, что функция обладает непрерывной и отличной от нуля производной на отрезке 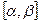. Геометрически гладкая кривая характеризуется тем, что в каждой точке она обладает касательной, причем угол наклона касательной к действительной оси, равный , непрерывно изменяется, когда точка касания перемещается вдоль по кривой.

Длина гладкой кривой определяется так:

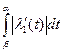
Так как модуль непрерывной функции на отрезке 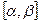также непрерывен на том же отрезке, что сразу следует из неравенства

,

где , то интеграл

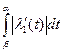
существует.

Более общий класс спрямляемых кривых представляют кусочно-гладкие кривые.

Непрерывная кривая называется кусочно-гладкой, если она составлена из конечного числа гладких кривых, или, выражаясь точнее, если для некоторого ее параметрического представления , отрезок 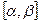может быть подразделен на конечное число отрезков , на каждом из которых функция обладает непрерывной и отличной от нуля производной. Из этого определения следует, что кусочно-гладкая кривая может и не иметь касательной в точках , но в каждой из этих точек существуют «левая» и «правая» касательные, так что указанные точки являются угловыми точками кусочно-гладкой кривой.

Простейшим примером кусочно-гладкой кривой может служить ломаная линия с конечным числом звеньев.

Длина кусочно-гладкой кривой определяется так:

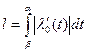
Кривая называется замкнутой, если ее начало совпадает с ее концом, то есть . В этом случае функцию можно считать непрерывной периодической функцией от действительного параметра с периодом , продолжив ее за пределы отрезка 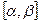с помощью равенства .

Если одна и та же точка 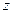кривой 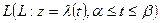соответствует двум или более различным значениям параметра , из которых, по крайней мере, одно отлично 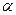от и от , то такая точка называется кратной. Кривая, не имеющая кратных точек, называется простой или жордановой кривой. Из этого определения следует, что в случае отсутствия самопересечений и самокасаний, непрерывная спрямляемая кривая будет жордановой кривой.

Имеет место

Поиск по сайту: