Расчет параметров сетевого графа

К параметрам сетевого графа относятся:

1. Продолжительность данной работы ();

2. Ранние параметры данной работы :

1) раннее начало работы ();

2) раннее окончание работы ()

3. Поздние параметры данной работы :

1) позднее начало работы ();

2) позднее окончание работы ()

4. Критический путь ()

5. Резервы:

1) полный резерв времени ();

2) частный резерв времени первого вида ();

3) частный резерв времени второго вида ();

4) свободный резерв времени ()

Для понимания взаимосвязей параметров сетевого графа, их соотношения и природы формирования резервов рассмотрим фрагмент сетевого графа, отражающего место данной работы на графе:

где – данная работа, ; ;

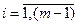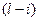– работа, непосредственно предшествующая данной работе ;

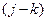– работа, непосредственно следующая за данной работой ;

события .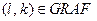

Известны два метода расчета параметров сетевого графа:

1) вычисление непосредственно на сетевом графе;

2) аналитический (табличный) способ.

Далее рассматриваются процедуры расчета параметров сетевого графа.

Порядок расчета параметров следующий:

1. Для каждой работы, принадлежащей сетевому графу, рассчитываются ее ранние параметры: сначала раннее начало, а затем – раннее окончание. В процессе расчета последовательно перебираются все без исключения работы, в том числе фиктивные. Расчет параметров ведется на графе – слева направо, а при работе с таблицей – сверху вниз.

Ранние параметры отражают сроки начала и окончания работ при предельно ранних возможностях их выполнения с учётом заданной последовательности работ: ,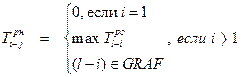

.

2. Определяется продолжительность критического пути.

Время критического пути определяется как суммарное время работ, лежащих на критическом пути, т.е. минимально возможное время, в продолжение которого завершится весь комплекс работ в соответствии с геометрией сетевого графа. Это время равно наибольшему времени ранних окончаний работ, входящих в конечное событие сетевого графа:

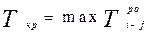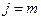, (конечное событие).

3. Для каждой работы, принадлежащей сетевому графу, рассчитываются ее поздние параметры: сначала позднее окончание, а затем – позднее начало. В процессе расчета последовательно перебираются справа налево на сетевом графе или снизу вверх при работе с таблицей все без исключения работы, в том числе фиктивные.

Поздние сроки начала и окончания работ определяются из возможностей предельного сдвига вправо на временной оси сроков выполнения работ в такой степени, чтобы не изменилась величина критического пути. Этим требованием обусловливается логика расчетов поздних параметров: от последнего события к первому и первоначальный расчет времени позднего окончания, а затем – позднего начала работы:

,

.

4. Расчет резервов сетевого графа.

Полный резерв времени (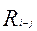) характеризуется предельным сдвигом вправо по временной шкале сроков выполнения работ сетевого графа. Его величина определяется разностью либо между поздним и ранним началами данной работы, либо между поздним и ранним ее окончаниями:

.

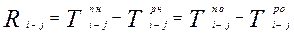Для работ критического пути , то есть у работ, лежащих на критическом пути, полный резерв времени равен нулю:

.

Руководствуясь этим правилом, можно выделить работы критического пути. При выделении работ сетевого графа, принадлежащих критическому пути следует руководствоваться следующими правилами:

· критический путь начинается с начального события и заканчивается конечным;

· каждая следующая включаемая в критический путь работа начинается с события, которым заканчивается непосредственно предшествующая ей работа, уже включенная в критический путь, поэтому не все работы, полный резерв времени у которых равен нулю, принадлежат критическому пути;

· формирование критического пути заканчивается, если в него включена работа, входящая в конечное событие.

В некоторых сетевых графах может быть не один, а несколько критических путей.

Частный резерв времени первого вида определяется возможностью изменения позднего начала работы () на более ранний срок без изменения поздних сроков окончания непосредственно предшествующих работ:

Частный резерв времени второго вида определяется возможностью изменения раннего окончания работы () на более поздний срок без изменения ранних сроков начала непосредственно следующих работ:

Свободный резерв времени работы 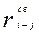определяется дополнительным временем (сверх продолжительности выполнения данной работы ()), которое находится в пределах ранних сроков начала непосредственно следующих и поздних сроков окончания непосредственно предшествующих работ:

Полный и частные резервы работы () будут равны, если конечное событие рассматриваемой работы является событием, лежащим на критическом пути.

Между полным резервом и частным резервом времени второго вида всегда имеет место соотношение: .

Следовательно:

1) если конечное событие () какой-либо работы () принадлежит критическому пути, то полный и частные резервы (первого и второго вида) будут равны;

2) если полный резерв некоторой работы равен нулю, то и частный резерв второго вида также равен нулю;

3) полный и частные резервы времени всегда являются положительным числом, то есть они больше или равны нулю;

4) для того, чтобы частный резерв времени работы () был равен нулю, необходимо и достаточно, чтобы эта работа лежала на пути максимальной длины от первого события до события . Событие может быть как промежуточным, так и конечным.

Поиск по сайту: