Если система замкнутая, ее передаточная функция

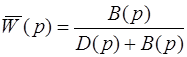. (5.4)

Характеристический полином есть D (p) + B (p). Устойчивость замкнутой системы определяется по характеристическому полиному D (p) + B (p). То есть, в нем содержится информация об устойчивости замкнутой системы. Отношение передаточных функций (2.6) и (5.4) есть отношение характеристического полинома замкнутой системы к характеристическому полиному разомкнутой системы:

.

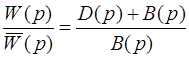Значит, содержит в себе информацию об устойчивости как замкнутой, так и разомкнутой системы. Устойчивость замкнутой системы связана с устойчивостью разомкнутой.

Поскольку

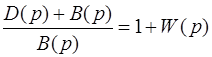, (5.10)

открываются возможности судить об устойчивости замкнутой системы по передаточной функции разомкнутой системы.

Запишем выражение (5.10) в частотной форме, полагая p = jw:

1 + W (jw).

W (jw) есть комплексная частотная характеристика разомкнутой системы. Эту характеристику можно изобразить графически на комплексной плоскости, задавая w от 0 до ∞ и рассчитывая частотные характеристики: действительную U(w) и мнимую V(w). Получается годограф разомкнутой системы. Его вид говорит об устойчивости или неустойчивости замкнутой системы.

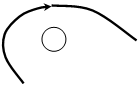
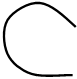
Допустим, разомкнутая система устойчива. Тогда, если годограф устойчивой разомкнутой системы при изменении w от 0 до ∞ не охватывает точку -1 на оси абсцисс, то замкнутая система будет устойчивой. Охватывает – замкнутая система неустойчивая.

Примеры годографов, соответствующих устойчивой и неустойчивой замкнутой системам, представлены на рис. 5.14 и 5.15.

V V

-1 -1

Рис. 5.14 Рис. 5.15

V V

-1 -1

Рис. 5.16 Рис. 5.17

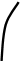
V V

-1 -1

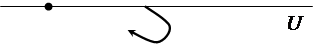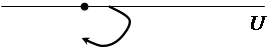
Рис. 5.18 Рис. 5.19

Замкнутая система может быть устойчивой и тогда, когда разомкнутая система неустойчива.

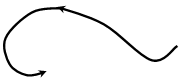
Критерий Найквиста для неустойчивой разомкнутой системы: если годограф неустойчивой разомкнутой системы при изменении w от 0 до ∞ охватывает точку -1 на оси абсцисс в положительном направлении m / 2 раз, где m – число корней характеристического уравнения разомкнутой системы с положительной действительной частью, то замкнутая система будет устойчивой. (положительной считается движение конца вектора против часовой стрелки).

Примеры годографов, соответствующих устойчивой и неустойчивой замкнутым системам во втором случае, представлены на рис. 5.16 и 5.17 для m = 2.

Если разомкнутая система имеет передаточную функцию, содержащую в знаменателе множителем комплексную переменную р,

,

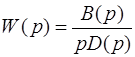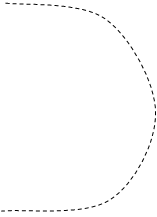
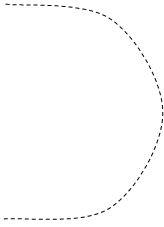
то комплексная частотная характеристика будет иметь неопределенность при w = 0. Амплитуда становиться бесконечной. Годограф получается с бесконечной ветвью. Но если годограф мысленно дополнить зеркально отраженной ветвью и провести полуокружность бесконечно большого радиуса так, чтобы она пересекала положительную часть оси абсцисс, то такой прием позволяет использовать первую формулировку критерия Найквиста. То есть, если точка -1 на оси абсцисс лежит за пределами замкнутой кривой – замкнутая система устойчивая. Если охватывается кривой – неустойчивая. Примеры таких годографов приведены на рис. 5.18 и 5.19.

Подведем итог сказанному в виде таблицы 1, с использованием соответствующих аббревиатур.

Таблица 1

РСУ. Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

РСН. Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

РС

астатическая. Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

Замкнутая система будет находиться на границе устойчивости, если годограф разомкнутой системы проходит через точку -1 оси абсцисс. Аналитически это условие можно записать в виде

1 + W (jw) = 0.

Кривые Найквиста наглядно показывают влияние коэффициента усиления на устойчивость системы. Для передаточной функции, в которой коэффициент усиления увеличивают, размеры и положение кривой Найквиста меняются относительно точки с координатой (-1,0). Допустим, имеется кривая 1, отвечающая границе устойчивости, рис.5.20. Предельный коэффициент усиления k = k ^*. Кривая 2, для которой k < k ^*, отвечает устойчивой системе, кривая 3, для которой

k > k ^* - неустойчивой. Увеличение коэффициента усиления вызывает смещение влево точки пересечения кривой 2 с отрицательной частью действительной оси. То есть, может перевести систему из устойчивого состояния в неустойчивое.

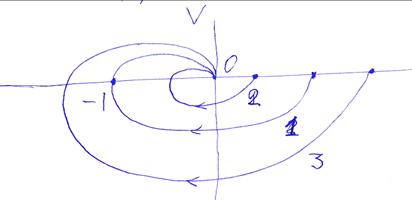
Рис. 5.20. Значение коэффициентов усиления:

1 - k = k ^*, 2 - k < k ^*, 3 – k > k ^*.

Система, имеющая годограф, изображенный на рис. 5.20, с увеличением коэффициента усиления способна реализовать два состояния: «устойчивость – неустойчивость». Для более сложных кривых число состояний может увеличиваться. Например, у кривой с одним максимумом в отрицательной полуплоскости (рис. 5.21) по мере

Рис. 5.21 Рис. 5.22

увеличения коэффициента усиления устойчивое состояние сменяется неустойчивым, а затем снова устойчивым. У кривой с двумя максимумами (рис.5.22), при увеличении коэффициента усиления, реализуются состояния: «устойчивость – неустойчивость – устойчивость – неустойчивость». Система может устойчиво работать в двух разных интервалах изменения коэффициента усиления. Это свойство не обнаруживается применением критерия Гурвица или Михайлова.

Коэффициент усиления на границе устойчивости рассчитывают, приравнивая комплексную частотную характеристику минус единице:

W (jw) = -1.

Поиск по сайту: