Теорема. Для будь-якої випадкової величини Х ймовірність того, що вона відхиляється від свого математичного сподівання більше

(Нерівність Чебишова)

Для будь-якої випадкової величини Х ймовірність того, що вона відхиляється від свого математичного сподівання більше, ніж на число 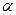, завжди менша, ніж 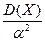, тобто:

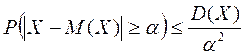(19)

У статистиці частіше використовують нерівність Чебишева для середнього квадратичного відхилення:

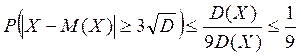
Граничні теореми які встановлюють відповідність між теоретичними та дослідними характеристиками випадкових подій. Об’єднують загальною назвою – закону великих чисел.

Нехай Х випадкова величина, яка має математичне сподівання М(Х) і дисперсію D(X). Нехай Х₁, Х₂,..., Х _п випадкові величини, які мають ті ж параметри розподілу, що й Х.

Візьмемо нову випадкову величину 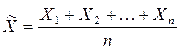. Застосуємо нерівність Чебишова для випадкової величини :

.

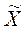Наслідком цієї нерівності є твердження: .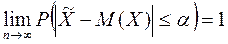

Тобто середнє арифметичне результатів випробування зі зростанням п все точніше відображає математичне сподівання досліджуваної випадкової величини.

Запитання для самоконтролю

1. Яку величину називають випадковою? Які є види випадкових величин? Навести приклади.

2. Що таке закон розподілу ДВВ? Назвати основні закони розподілу ДВВ.

3. Які існують числові характеристики дискретних випадкових величин? Що вони означають та за якими формулами обчислюються?

4. Дати визначення інтегральної та диференціальної функції розподілу. Вказати властивості та взаємозв’язок між ними.

5. Назвати основні закони розподілу НВВ.

6. За якими формулами обчислюють числові характеристики для НВВ?

7. Записати нерівність Чебишова в двох формах.

Поиск по сайту: