Несобственные интегралы

Пусть функция 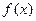определена при всех 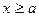и интегрируема по Риману на каждом из отрезков 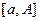. Положим

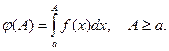
Определение 1. 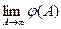(конечный или бесконечный) называют интегралом функции от 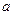до 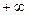и обозначают символом 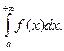Если этот предел конечен, то про интеграл 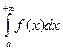говорят, что он сходится, а функцию называют интегрируемой в бесконечном промежутке .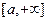

Если же 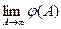бесконечен или вовсе не существует, то говорят, что несобственный интеграл 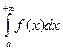расходится.

В отличие от интеграла Римана, только что определенный интеграл называется несобственным интегралом первого рода.

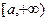Теорема 1. Если функция обладает примитивной на промежутке , то интеграл 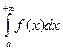сходится тогда и только тогда, когда существует конечный предел .

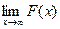Пример 1. Пусть 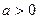. Несобственный интеграл 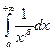сходится тогда и только тогда, когда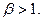

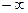Аналогично определяется интеграл функции от до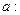

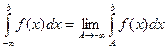
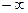Интеграл функции от до 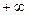определяют равенством

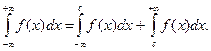
Определение 2. Пусть функция 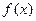непрерывна во всех точках отрезка 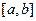, за исключением точки 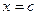, где она имеет разрыв ІІ рода (бесконечный разрыв). Положим

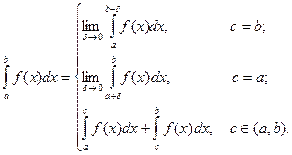
Этот интеграл называют несобственным интегралом ІІ рода. В первых двух случаях несобственный интеграл второго рода называется сходящимся, если пределы, указанные в его определении, конечны. Если эти пределы бесконечны или вовсе не существуют, то несобственный интеграл второго рода называется расходящимся. В третьем случае

несобственный интеграл называется сходящим, если сходятся оба интеграла 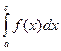и, 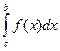, указанные в его определении. В противном случае его называют расходящимся.

Пример 2. Пусть 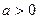. Несобственный интеграл второго рода 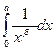сходится тогда и только тогда, когда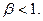

Поиск по сайту: