 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифракционный интеграл, основные положения и формулы
Дифракционный интеграл в точной формулировке был записан Кирхгофом в 1882 году. [1] Он явился точной формулировкой ранее выдвинутой идеи, называемой принципом Гюйгенса. Эта идея была развита Френелем. Напомним, что согласно принципу Гюйгенса каждая точка волновой поверхности может рассматриваться как самостоятельный точечный источник сферической волны.
Дифракционным интегралом называют интегральное преобразование, которое позволяет выразить распределение поля в некоторой области пространства через известное распределение поля на заданной поверхности. В частности, в когерентной оптике дифракционный интеграл применяется для того, чтобы выразить распределение амплитуд поля 
в плоскости П2, находящейся на расстоянии 
от плоскости П1, через распределение амплитуд поля 
в первой плоскости П1, т.е. через распределение поля на излучающей апертуре (рис3.1.)
Рис 3.1 Схема, иллюстрирующая расчеты с помощью дифракционного интеграла.
При этом в оптических задачах учитывают ряд обстоятельств, которые значительно упрощают общий вид дифракционного интеграла:
-излучающую поверхность (апертуру) обычно полагают плоской;
-принимают во внимание то обстоятельство, что длина волны l оптического излучения очень мала по сравнению с расстоянием r от точки на излучающей апертуре до точки на плоскости наблюдения и ставят условие: 
Это условие называют оптическим приближением.
С учетом определенных, упомянутых выше приближений, можно записать выражение для искомой функции распределения поля 
в плоскости П2 
на расстоянии 
от плоскости П1 (
, z = 0) через распределение поля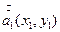 
в этой плоскости в виде:
, (3.1)
В этой формуле 
- площадь апертуры, ds – элемент площади 
, 
,
r – текущий радиус вектор между точкой с координатами x 1, y 1 в плоскости П1 и точкой x 2, y 2 с координатами в плоскости П2 (рис. 3.1).
Далее используют так называемое параксиальное приближение, при котором полагают, что размер апертуры излучения мaл по сравнению с расстоянием между плоскостью апертуры и плоскостью наблюдения. При условии, что координаты x 1 и y 1, а также x 2, y 2 изменяются лишь в сравнительно небольшой ограниченной области, т.е.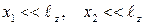 
и 
, и аналогично 
, можно положить, что величина r изменяется очень мало. В этом случае мы не допустим большой ошибки, если в знаменателе дроби под интегралом в выражении (3.1) заменим переменную величину r на постоянную величину , которая является постоянной, не зависящей от переменных интегрирования. Выведем эту величину за знак интеграла, положив 
. В то же время в показателе экспоненты такую замену сделать нельзя. Величину r в показателе экспоненты представим в виде квадратного корня из суммы квадратов координат, который затем преобразуем с учетом предполагаемой малости отношений 
и 
:
. (3.2)
Из (3.1) и (3.2) получим следующее выражение, связывающее распределение комплексных амплитуд поля в плоскости П2 через распределение комплексных амплитуд в плоскости П1.
. (3.3)
Интересно отметить, что по форме записи интеграл (3.3) представляет собой свертку функции распределения 
с функцией вида 
.
Формула (3.3) содержит в показателе экспоненты квадратичные члены и отражает случай так называемой дифракции Френеля.
3.2. Предельный переход к дифракции Фраунгофера.
В формуле (3.3) преобразуем разности квадратов в степени экспоненты подынтегрального выражения. Представим интеграл (3.3) в следующем виде:
(3.4)
В этом выражении множитель, содержащий в показателе экспоненты величины 
и 
вынесен за знак интеграла, так как х 2 и у 2 не являются переменными интегрирования. При некотором дополнительном условии подынтегральное выражение можно упростить, положив, что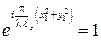 
. Это справедливо при условии, что показатель степени экспоненты очень мал, т.е. при условии:
. (3.5)
Рассмотрим пример, когда апертура представляет собой квадратную площадку размером стороны, равном D. В этом случае величина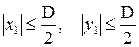 
, а наибольшие значения переменных x, y будут следующими: 
.
С учетом этого условия формулу (3.5) можно записать:
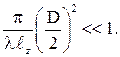(3.6)
Отсюда следует условие
. (3.7)
Приближенно это условие записывают в виде:
. (3.8)
При этом условии, которое называют условием перехода к дальней зоне поля излучения, а по другой терминологии к зоне Фраунгофера, интеграл (3.4) имеет следующий вид:
. (3.9)
Перед интегралом мы имеем ряд множителей. Группа множителей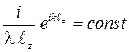 
является константой, которая не зависит от координат х 2, у 2. Множитель 
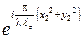является чисто фазовым, он описывает параболическую кривизну волнового фронта в плоскости 
.
Двойной интеграл по площади апертуры SA можно преобразовать к виду, который будет фактически преобразованием Фурье от распределения амплитуд поля на апертуре 
. С этой целью сделаем следующие преобразования:
во-первых: распространим пределы интегрирования на всю плоскость х 1 у 1, т.е. от 
до 
. Это можно сделать, так как за пределами апертуры поле излучения отсутствует 
при 
;
во-вторых: величины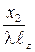 
и 
преобразуем следующим образом:
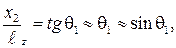(3.10)
(3.11)
Это приближение можно считать допустимым при малых величинах углов q1 и q2. Напомним, что мы ранее приняли условие о том, что рассматривается параксиальное приближение. При этом углы дифракции, q1, q2 мы полагаем малыми. Тогда с учетом (3.10) и (3.11) можно записать:
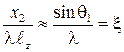. (3.12)
. (3.13)
Здесь x и h в соответствии с ранее данными определениями являются пространственными частотами.
Расширим пределы интегрирования за пределы апертуры, до бесконечности, учитывая, что за пределами апертуры амплитуда поля равна нулю. В результате с учетом (3.12) и (3.13) интеграл (3.9) можно записать в виде:
. (3.14)
Интеграл в выражении (3.14) представляет собой двумерное преобразование Фурье распределения поля на апертуре.
Если мы поставим задачу исследовать распределение интенсивности (плотности мощности) в дальней зоне, то из выражения (3.14) получим
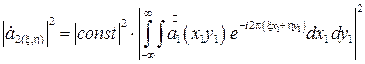, (3.15)
т.е. распределение мощности излучения с точностью до постоянного множителя представляет собой спектр мощности излучения с апертуры.
Составим модель проведения эксперимента по наблюдению пространственного спектра мощности. Рассмотрим простой пример. Допустим, что плоская когерентная волна проходит через квадратное отверстие размером 1мм. на 1мм. Длина волны излучения равна 0,63 микрометра.
Найдем расстояние до области дальней зоны:
Расположим экран на расстоянии, 
, например на расстоянии 4 метра от отверстия. Будем исследовать распределение плотности мощности излучения на экране. Напомним, что ранее при анализе спектра дифрагированных волн, исходящих от щели с размером, равным D было получено выражение:
При условии, что апертура ограничена также и в направлении координаты Y
Получим для излучения с квадратной апертуры: 
На экране мы увидим центральное пятно, обрамленное побочными максимумами в направлениях координат X и Y. Рассчитаем координаты первых нулей 
. Положим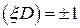 
, тогда 
= 
.
Отсюда получим: 
Аналогично получим 
3.3 Анализ оптической схемы из транспаранта и линзы.
3.3.1.Функция пропускания тонкой линзы. Для анализа нам необходимо будет описать функцию прозрачности линзы, т.е. функцию преобразования волнового фронта при прохождении его через тонкую линзу. С этой целью рассмотрим оптическую схему, изображенную на рис. 3.3.
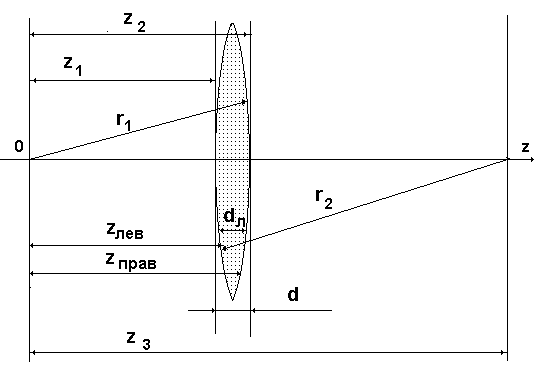
Рис 34. 3 Схема для расчета фазовой задержки оптической волны в линзе.
Тонкая линза, изготовленная из прозрачного материала с показателем преломления, равным 
, окружена воздухом с показателем преломления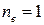 
. Толщина линзы 
намного меньше, чем радиусы поверхностей r 1 и r 2, образующие линзу. Важное условие состоит в том, что материал линзы прозрачен и не поглощает излучения. При отсутствии поглощения линза представляет собой фазовый транспарант, функцию пропускания которого 
можно выразить в виде:
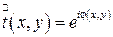(3.16)
Здесь функция 
отражает зависимость фазовой задержки оптической волны от координат x и y при ее прохождении от плоскости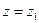 
до плоскости 
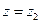, касательных плоскостей к выпуклостям линзы.
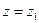Проведем расчет фазовой задержки , которая складывается из фазовой задержки в толще материала линзы c показателем преломления и фазовой задержки в воздушных промежутках между поверхностями, образующими линзу, и плоскостями и 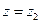. Толщину линзы, d л (х, у), в произвольной точке с координатами х и у найдем, рассчитав разность между координатами z правой и левой сферических поверхностей.
d л (х, у) = 
, (3.17)
где
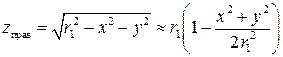, (3.18)
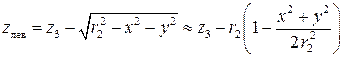. (3.19)
Здесь z 3 – координата центра сферы с радиусом r 2 по отношению к точке 
, где расположен центр сферы с радиусом r 1.
Замена квадратного корня приближенным выражением справедлива в случае параксиального приближения. При этом предполагается,
что 
. С учетом сделанных приближений толщина материала линзы в области с координатами 
составит:
d л (х, у)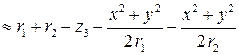 
. (3.20)
Фазовая задержка световой волны с длиной волны l в материале
линзы составит:
. (3.21)
Фазовая задержка в воздушном промежутке 
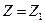между плоскостями 
и 
и поверхностями линзы составит:
, (3.22)
где d - расстояние между плоскостям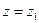и и 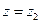, а величина 
- длина воздушного промежутка.
Суммируя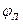 
и 
, найдем полный фазовый сдвиг световой волны при ее прохождении от плоскости 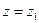до плоскости 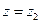, он составит:
. (3.23)
Второе слагаемое не зависит от координат х, у и фактически обозначает неизменный фазовый сдвиг при прохождении волны от одной плоскости до другой. Поскольку этот сдвиг равносилен изменению начала отсчета световой волны, он не влияет на функции преобразования волнового фронта в оптической схеме, и его можно отбросить. После этого с учетом формулы (3.20) получим следующую формулу, выражающую зависимость фазового запаздывания волны в тонкой линзе от координат х, у.
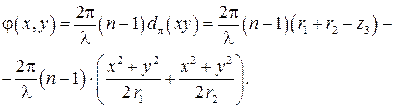(3.24)
В этом выражении первое слагаемое также представляет постоянный фазовый сдвиг, не зависящий от переменных х, у. Отбросив это слагаемое, получим:
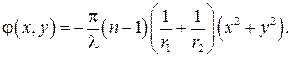(3.25)
Из геометрической оптики известно соотношение, связывающее оптическую силу линзы Dл с радиусами сферических поверхностей, образующих линзу.
(3.26)
С учетом выражений (3.25) и (3.26) формулу, характеризующую комплексную функцию пропускания линзы (3.16) можно записать в такой форме:
(3.27)
Следовательно, тонкая линза является фазовым транспарантом, который преобразует волну с плоским фронтом (на входе слева) в волну с волновым фронтом в форме параболоида вращения.
Поиск по сайту: