Скалярне поле. Похідна за напрямком

Означення 3.2. Область простору, кожній точці М якої за певним правилом поставлено у відповідність одне єдине значення деякої скалярної фізичної величини 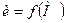, називається скалярним полем величини и.

Прикладами скалярних полів є поле густини даного неоднорідного середовища, поле вологості повітря, поле температури даного тіла, поле атмосферного тиску, поле потенціалів заданого електростатичного поля.

Якщо функція 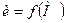не залежить від часу, то скалярне поле називають стаціонарним. Якщо ж и залежить від часу, то скалярне поле називають нестаціонарним.

Наприклад, коли в середовище, яке проводить тепло, помістити нагріте тіло, то воно буде з часом охолоджуватися. Температура в точках цього середовища залежатиме від розглядуваної точки та від плину часу. Отже, матимемо нестаціонарне поле температур.

Надалі розглядатимемо лише стаціонарні поля.

Зауваження 3.4. Означення скалярного поля не відрізняється від означення функції. Термін „поле” перенесено з фізики і підкреслює походження розглядуваного поняття.

Якщо в просторі ввести прямокутну декартову систему координат xOyz, то точка М матиме в цій системі певні координати 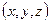і скалярне поле и стане функцією цих координат:

.

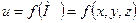У випадку, коли скалярна функція 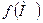залежить тільки від двох змінних, наприклад х та у, то відповідне скалярне поле 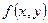називають плоским. Наприклад, поле температури навколо необмеженого в обох напрямках рівномірно нагрітого прямолінійного дроту є плоским. Якщо ж функція 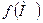залежить від трьох змінних х, y та z, то скалярне поле називають просторовим.

Геометрично плоскі скалярні поля зображають за допомогою ліній рівня, а просторові – за допомогою поверхонь рівня.

Однією з найважливіших характеристик скалярного поля є похідна за напрямком. З¢ясуємо це поняття.

Нагадаємо, що для функції однієї змінної 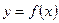похідна 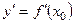виражає швидкість зміни цієї функції в точці 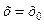. Отже, частинні похідні

, ,

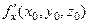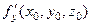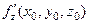
виражають швидкість зміни функції (поля) відповідно в напрямках, паралельних координатним осям.

Тому природньо поставити питання про швидкість зміни функції в точці 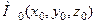в довільному напрямку, що виходить з цієї точки.

Нехай задано скалярне поле , причому область визначення функції є відкритою та зв¢язною. Розглянемо якийсь фіксований вектор , який утворює з додатними напрямками координатних осей відповідно кути 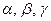. Зафіксуємо в скалярному полі точку 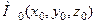і візьмемо в цьому полі довільну точку 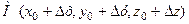, таку щоб вектор 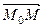був співнапрямленим з вектором .

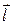Позначимо .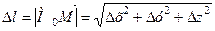

При переході від точки М ₀ до точки М функція 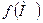отримає приріст в напрямі вектора , який дорівнює

.

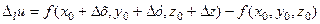Означення 3.3. Якщо існує скінченна границя відношення 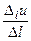при , то ця границя називається похідною функції (поля) 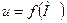в точці 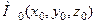за напрямком вектора 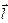і позначається

.

Теорема 3.1. Якщо функція 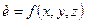диференційована в точці 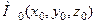, то в цій точці існує похідна функції 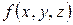за напрямком вектора і

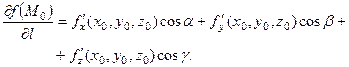. (3.9)

Д о в е д е н н я. Перш ніж приступити до доведення теореми, зауважимо, що рівність (3.9), яку потрібно довести можна переписати ще й так:

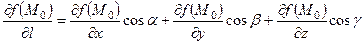.(3.10)

За умовою теореми функція 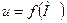диференційована в точці М ₀, тому її приріст 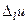в цій точці можна записати у вигляді

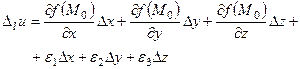, (3.11)

де 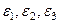- нескінченно малі функції при .

Оскільки вектор співнапрямлений з вектором 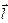, то

.

Тому, підставивши це в рівність (3.11) і розділивши обидві частини (3.11) на 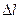, отримаємо

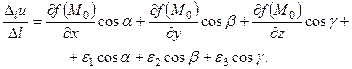
Перейшовши тут до границі при , дістанемо рівність (3.10).

Теорему доведено.

Відзначимо, що рівність (3.10) в довільній точці М записуватимемо коротко у вигляді

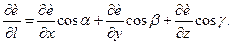(3.12)

Зауваження 3.4. Згідно означення 3.3, частинні похідні 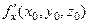, , 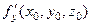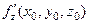можна розглядати як похідні функції 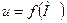за напрямками відповідно 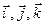в точці 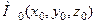. Дійсно, наприклад, якщо 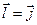, то , тому 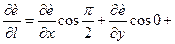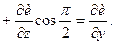Отже, похідна за напрямком є узагальненням поняття про частинну похідну.

Відзначимо, що абсолютна величина 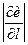відповідає значенню швидкості зміни скалярного поля в точці , а знак похідної визначає характер зміни в напрямку 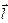(зростання чи спадання).

Легко бачити, що при зміні напрямку на протилежний 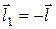похідна за напрямком також змінить свій знак.

Дійсно, при зміні напрямку на протилежний кути 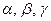зміняться на 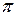, тому

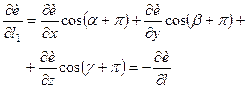. (3.13)

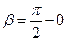Зауваження 3.5. Якщо поле плоске, тобто задається функцією , то напрям вектора однозначно визначається кутом , а , . З врахуванням цього рівність (3.11) набуде вигляду

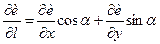. (3.14)

Розглянемо приклади.

Приклад 3.3. Знайти похідну функції 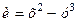в точці 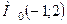за напрямком 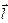, який утворює кут 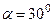з додатним напрямком осі Ох.

Р о з в′ я з а н н я

Знаходимо частинні похідні в заданій точці:

,

.

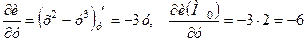Тоді, скориставшись формулою (3.14), матимемо:

.

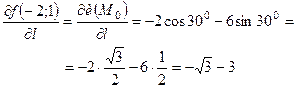Як ми бачимо, 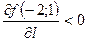, тому наша функція в заданому напрямку спадає.

Приклад 3.4. Знайти похідну функції 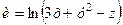в точці 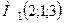за напрямком від цієї точки до точки .

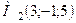Р о з в′ я з а н н я

В нашому випадку вектор 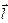та його довжина дорівнюють:

,

.

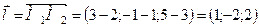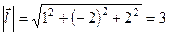Значить, напрямні косинуси будуть такими:

Тепер знайдемо частинні похідні та обчислимо їхні значення в точці М ₁.

;

;

.

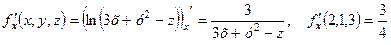Підставивши обчислені значення в (3.10), знаходимо шукану похідну в точці М ₁ в заданому напрямку:

.

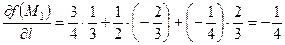Поиск по сайту: