 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Логика высказываний
3.1.Введение
Алгебра логики (логика высказываний) – это раздел дискретной математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними.
Алгебра логики возникла в середине 19 в. в трудах Дж. Буля и развивалась затем в работах Ч. Пирса, П. С.Порецкого, Б. Рассела, Д. Гильберта и др. Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами.
С появлением теории множеств (70-е гг. 19 в.), поглотившей часть первоначального предмета алгебры логики, и дальнейшим развитием математической логики (последняя четверть 19 в. - 1-я половина 20 в.) предмет алгебры логики значительно изменился. Основным предметом алгебры логики стали высказывания.
3.2.Основные понятия
В формально-логических выводах используются истинные и ложные предложения.
Определение: повествовательное предложение, о котором можно однозначно сказать, истинно оно или ложно, называется высказыванием.
Примеры высказываний: "кит - животное", "все углы - прямые" и т. п. Первое из этих высказываний является, очевидно, истинным, а второе - ложным. Предложение "реши задачу", также как и "2+2", не является высказываем.
Определения математических понятий не являются высказываниями, т.к. это принятые соглашения.
Будем обозначать высказывания большими латинскими буквами: A, B, C,….
Элементарные, нерасчленяемые высказывания будем называть атомами.
3.3.Логические операции.
Употребляемые в обычной речи логические связки "и", "или", "если..., то...", "эквивалентно", частица "не" и т. д. позволяют из уже заданных высказываний строить новые, более "сложные" высказывания.
Аналогично тому, как в языке из простых предложений с помощью логических связок образуются сложные предложения, так и в логике высказываний из атомов можно образовывать составные высказывания.
Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.
Рассмотрим определения логических операций, соответствующих логическим связкам.
Каждому высказывания можно сопоставить его истинностное значение, обозначаемое соответственно через И (если высказывание истинно), Л (если высказывание ложно).
Истинностное значение сложных высказываний зависит от истинностных значений высказываний, составлявших слоеное высказывание.
Эта зависимость устанавливается в данных ниже определениях я стращается в таблицах истинности.
Пусть A, В - произвольные высказывания, относительно которых не предполагается, что известно их истинностные значения.
Связке "НЕ" соответствует логическая операция отрицания, обозначение операции – знак ù или  .
.
Определение. Отрицанием высказывания A называется высказывание 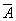 (ùA), которое истинно, если A – ложно, и ложно, если A – истинно.
(ùA), которое истинно, если A – ложно, и ложно, если A – истинно.
Таблица истинности отрицания:
| A | 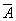
|
| И | Л |
| Л | И |
Пример: A: 2*2=4 – истинное высказывание; 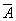 :
: 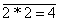 или 2*2
или 2*2  4 - ложное высказывание.
4 - ложное высказывание.
Связке "И" соответствует операция конъюнкция, обозначение операции – знак  (или &).
(или &).
Определение. Конъюнкцией высказываний A и B называется высказывание A  B (читается "A и B"), которое истинно тогда и только тогда, когда A, B – истинно.
B (читается "A и B"), которое истинно тогда и только тогда, когда A, B – истинно.
Таблица истинности конъюнкции:
| A | B | A  B B
|
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Пример: A: 5 – нечетное число; B: Пушкин родился в 1799 г – истинные высказывания; поэтому высказываниеA  B: 5 – нечетное число
B: 5 – нечетное число  Пушкин родился в 1799 г. – истинное высказывание.
Пушкин родился в 1799 г. – истинное высказывание.
Связке "ИЛИ" соответствует операция дизъюнкция, обозначение операции – знак  .
.
В формально-логических выводах «или» употребляется не в исключающем смысле (в отличие от обыденной речи, где эта связка может употребляться и в исключающем смысле и в неисключающем смысле)
Определение. Дизъюнкцией высказываний A и B называется высказывание A  B (читается "A или B"), которое ложно тогда и только тогда, когда A, B – ложны.
B (читается "A или B"), которое ложно тогда и только тогда, когда A, B – ложны.
Таблица истинности дизъюнкции:
| A | B | A  B B
|
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Пример. A: 7<10, и.в. В: 3 - число четное, л.в. A  B: 7<10
B: 7<10  3 - число четное, и.в.
3 - число четное, и.в.
Связке "ЕСЛИ....ТО" соответствует логическая операция импликация, обозначение операции знак →.
Определение. Импликацией высказываний A и B называется высказывание A→B (читается "если A, то B"), которое ложно тогда и только тогда, когда A – истинно, а B – ложно.
Таблица истинности импликации:
| A | B | A→B |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Пример. A: 2*2=5, л. в. В: 2=2, и. в. A→B: 2*2=5→ 2=2. и. в.
Высказывание A называется условием или посылкой, высказывание В - заключением или следствием импликации.
Связке "ТОГДА И ТОЛЬКО ТОГДА, КОГДА" соответствует операция эквиваленция, обозначение операция – знак «.
Определение. Эквиваленцией высказываний A и В навивается высказывание, обозначаемое A«B (читается:"Aтогда и только тогда, когда В" или короче: "A эквивалентно В"), которое считается истинным только тогда, когда оба высказывания A и В имеют одинаковое истинностное значение.
Эквивалентность А«В читается также следующим образом: "Для того, чтобы A, необходимо и достаточно, чтобы В".
Таблица истинности эквиваленции:
| A | B | A«B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
Пример. A: 7 – число простое; и.в. В: в равнобедренном треугольнике при основании углы равны, и.в. A«В - и.в.
3.4.Составные высказывания
С помощью рассмотренных в предыдущем пункте логических операций из заданной совокупности атомов (элементарных высказываний) можно строить различимо составные высказывания. Порядок выполнения действий указывается скобками.
Истинностное значение составного высказывания зависит только от истинностных значений образующих его атомов, оно может быть найдено на основании определение логических операций с помощью таблиц истинности.
Пример.  .
.
| A | B | C | 
| 
| 
|
| И | И | И | И | Л | И |
| И | И | Л | И | Л | Л |
| И | Л | И | Л | И | И |
| И | Л | Л | Л | И | И |
| Л | И | И | Л | И | И |
| Л | И | Л | Л | И | И |
| Л | Л | И | Л | И | И |
| Л | Л | Л | Л | И | И |
3.5.Формулы логики высказываний
Основная задача логики высказываний состоит в изучении логических форм составных высказываний с помощью логических операций.
Понятие логической формы составного высказывания уточняется с помощью вводимого понятия формулы логики высказываний.
Понятие формул логики высказываний определяется следующим образом:
1. Элементарные формулы – атомы – являются формулами логики высказываний.
2. Если A, B – формулы, то 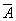 , (A
, (A  B), (A
B), (A  B), (A→B), (A«В) также являются формулами логики высказываний.
B), (A→B), (A«В) также являются формулами логики высказываний.
3. только те выражения являются формулами логики высказываний, для которых это следует из 1, 2.
Согласно определения, всякая формула либо атом, либо образуется из атомов в результате применения 2.
Число скобок в формулах можно уменьшить, если опустить внешнюю пару скобок и упорядочить знаки логических операций по старшинству: «, →,  ,
,  ,
,  .
.
Знак «имеет самую большую область действия, знак  самую маленькую.
самую маленькую.
Определение. Формулы логики, принимающие значение "истина" при любых значениях атомов, входящих в формулу, называется тождественно истинными (или законами логики, или тавтологиями).
Например, формула  всегда тождественно истинна.
всегда тождественно истинна.
Определение. Формулы логики, принимающие всегда ложное значение, называются тождественно ложными (или противоречиями).
Например, формула  - противоречие.
- противоречие.
Определение. Формулы алгебры логики, принимающие значение «ложь» хотя бы на одном наборе значений атомов, входящих в формулу называются опровержимыми.
Определение. Формулы алгебры логики, принимающие значение «истина» хотя бы на одном наборе значений атомов, входящих в формулу называются выполнимыми.
Определение. Формулы Р и Q называются равносильными, если их истинностные значения совпадают при любом выборе истинностных значений атомов, входящих в эти формулы.
Запись Р  Q означает, что формулы Р и Q равносильны.
Q означает, что формулы Р и Q равносильны.
3.6.Законы логики (свойства логических операций)
Следующие формулы являются законами логики.
1.  - закон двойного отрицания.
- закон двойного отрицания.
2.  - закон коммутативности конъюнкции.
- закон коммутативности конъюнкции.
3.  - закон коммутативности дизъюнкции.
- закон коммутативности дизъюнкции.
4.  - закон ассоциативности конъюнкции.
- закон ассоциативности конъюнкции.
5. 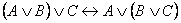 - закон ассоциативности дизъюнкции.
- закон ассоциативности дизъюнкции.
6.  - закон дистрибутивности конъюнкции относительно дизъюнкции.
- закон дистрибутивности конъюнкции относительно дизъюнкции.
7.  - закон дистрибутивности дизъюнкции относительно конъюнкции.
- закон дистрибутивности дизъюнкции относительно конъюнкции.
8. 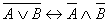 - закон отрицания дизъюнкции.
- закон отрицания дизъюнкции.
9.  - закон отрицания конъюнкции.
- закон отрицания конъюнкции.
10.  - закон отрицания импликации.
- закон отрицания импликации.
11.  - закон выражения эквивалентности через конъюнкцию и импликацию.
- закон выражения эквивалентности через конъюнкцию и импликацию.
12.  - закон контрапозиции.
- закон контрапозиции.
13.  - закон силлогизма.
- закон силлогизма.
Для доказательства любого из приведенных выше законов можно использовать следующие способы:
1. Построить таблицы истинности для левых и правых частей эквивалентности и убедиться, что получены одинаковые значения для всех значений атомов.
2. Построить значение всей формулы и убедится, что формула является тавтологией.
Пример. Докажем закон отрицания конъюнкции ( ) этими способами:
) этими способами:
1. Найдем значения для  и
и  и сравним их.
и сравним их.
| A | B | 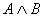
| 
| 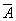
| 
| 
|
| И | И | И | Л | Л | Л | Л |
| И | Л | Л | И | Л | И | И |
| Л | И | Л | И | И | Л | И |
| Л | Л | Л | И | И | И | И |
2. Найдем значение  и убедимся, что при всех значениях A и B - это истинное значение.
и убедимся, что при всех значениях A и B - это истинное значение.
| A | B | 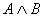
| 
| 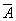
| 
| 
| 
|
| И | И | И | Л | Л | Л | Л | И |
| И | Л | Л | И | Л | И | И | И |
| Л | И | Л | И | И | Л | И | И |
| Л | Л | Л | И | И | И | И | И |
3.7.Логическое следствие
Определение. Формула B есть логическое следствие формул A1, A2,.., An, если формула B принимает истинное значение при тех же значениях, при которых истинна каждая из формул A1, A2,.., An.
Запись (A1, A2,.., An)ÞB означает, что B – логическое следствие формул A1, A2,.., An.
Пример. (A®B, A®  )Þ
)Þ 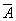 .
.
Докажем данное следствие.
| A | B | A®B | 
| A® 
| 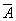
|
| И | И | И | Л | Л | Л |
| И | Л | Л | И | И | Л |
| Л | И | И | Л | И | И |
| Л | Л | И | И | И | И |
Из определения следует, что противоречие логически влечет любую формулу, а тавтология логически следует из любой формулы логики.
Определение. Формулы F и G называются равносильными, если они являются логическими следствиями друг друга. Обозначение:  .
.
Проанализировав последнее определение, получаем, что формулы равносильны, если они на всех наборах значений переменных превращаются в одинаковые по истинностному значению высказывания.
Следующие теоремы связывают логическое следствие и импликацию, равносильность и эквиваленцию.
Теорема1.  тогда и только тогда, когда A®B – тавтология.
тогда и только тогда, когда A®B – тавтология.
Теорема2.  тогда и только тогда, когда A«B – тавтология.
тогда и только тогда, когда A«B – тавтология.
Поиск по сайту: