 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дії над коренями
|
Читайте также: |
Додавання, віднімання - виявити подібні доданки і звести їх.
Наприклад:  .
.
Множення і ділення радикалів. Потрібно перемножити чи поділити підкореневі вирази і записати їх під знаком радикала.
Наприклад:  .
.
При множенні і діленні радикалів з різними показниками, їх треба звести до одного показника.
Піднесення до степеня.
Наприклад: 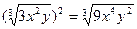 .
.
Добування кореня з радикалів. З підкореневого виразу треба добути корінь з показником, що дорівнює добутку двох даних показників.
Наприклад:  .
.
Знищення ірраціональності – домножити чисельник і знаменник на один і той же вираз (Наприклад:  .); домножити вираз на спряжений (Наприклад:
.); домножити вираз на спряжений (Наприклад: 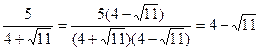 .)
.)
Лекція 14.
Тема: Ірраціональні рівняння і нерівності. Системи їх.
План.
1. Означення ірраціонального рівняння.
2. Основний спосіб розв’язування рівнянь цього виду.
3. Виникнення сторонніх коренів.
4. Приклади розв’язування рівнянь.
5. Системи ірраціональних рівнянь.
6. Ірраціональні нерівності.
Рівняння, в яких невідоме міститься під знаком радикала називається ірраціональним.
Наприклад: 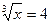 .
.
Основний спосіб розв’язування рівнянь цього виду- зведення їх до раціонального. Цього можна досягнути, якщо піднести обидві частини рівняння до відповідного степеня.
Наприклад: 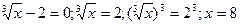 .
.
Наприклад:  Оскільки, невідоме знаходиться під знаком кореня 4-го степеня, переконаємось, що при -1 та 2 дані корені існують.
Оскільки, невідоме знаходиться під знаком кореня 4-го степеня, переконаємось, що при -1 та 2 дані корені існують.
Перевірка: при х=-1 вираз не має смислу, отже х=-1-сторонній корінь; х=2 задовольняє умови виразу, тому є коренем рівняння.
Після піднесення обох частин рівняння до степеня може підвищитись степінь даного рівняння, а разом з підвищенням степеня збільшується кількість коренів. Можуть з’явитись сторонні корені, що не задовольняють рівняння.
Знайшовши корені ірраціонального рівняння, необхідно виконати перевірку їх.
Приклади розв’язування рівнянь.
1) Піднесення до квадрата обох частин рівняння.
Наприклад:

Перевірка: х=4-сторонній корінь.
Відповідь: х=-1.
2) Піднесення до квадрата двічі.
Наприклад:
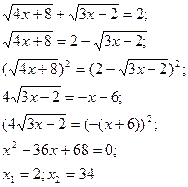
Обидва корені – сторонні.
Відповідь: коренів немає.
3) Піднесення до третього степеня.
Наприклад:
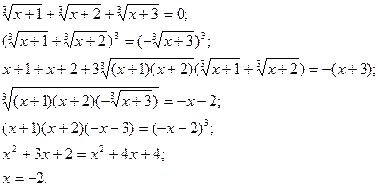
Відповідь:-2.
4) Введення допоміжної змінної.
Наприклад:

Відповідь: 1 і 27.
Системи ірраціональних рівнянь зводять до раціональних тими ж способами, що і рівняння.
Наприклад: розв’язати систему ірраціональних рівнянь
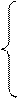 | 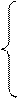 | 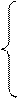 | 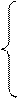 |




Відповідь: (4;9);(9;4).
Метод інтервалів - універсальний при розв’язуванні ірраціональних нерівностей.
Наприклад: розв’язати нерівність
 розглянемо функцію
розглянемо функцію  .
.
 Знайдемо область її визначення 15-х>0; х<15. Знайдемо нулі функції, тобто ті значення змінної, при яких значення функції дорівнює нулю
Знайдемо область її визначення 15-х>0; х<15. Знайдемо нулі функції, тобто ті значення змінної, при яких значення функції дорівнює нулю
 |  |  |

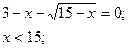



 |
+ -
-1 15 х
Відповідь: (-1;15).

Лекція 15.
Тема: Степінь з раціональним показником та його властивості.
План.
1.Степінь з натуральним та цілим показником.
2. Степінь з раціональним показником.
3. Степінь з ірраціональним показником.
1.Степінь з натуральним та цілим показником.

Властивості:


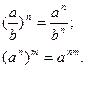
2. Степінь з раціональним показником.
Якщо 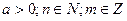 , то степінь числа
, то степінь числа  з дробовим показником
з дробовим показником 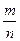 є радикал
є радикал  ; отже,
; отже,  .
.
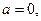 то
то 

 -парне,
-парне,  - непарне, то вираз
- непарне, то вираз  не має смислу.
не має смислу.
Наприклад:  .
.
Степенем  невід’ємного числа
невід’ємного числа  називають невід’ємне число,
називають невід’ємне число,  -й степінь якого дорівнює
-й степінь якого дорівнює  , тобто,
, тобто, 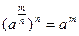 .
.
Властивості:

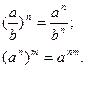
3.Степінь з ірраціональним показником.
 ірраціональне.
ірраціональне.
 .
.
 - під степенем
- під степенем  розуміють число, менше
розуміють число, менше 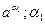 - з недостачею; або більше
- з недостачею; або більше  - з надлишком.
- з надлишком.
 .
.
Лекція 16.
Тема: Степенева функція. Її графік і властивості.
Функцію  , де р-стале дійсне число, а х(основа)- змінна називають степеневою функцією.
, де р-стале дійсне число, а х(основа)- змінна називають степеневою функцією.
1.р-натуральне
р-непарне р-парне
 | |||
 | |||
у у
 |  |
х х
2.р-ціле
р-непарне р-парне
 |

 у у
у у
 |
 х
х
 |
х
3.р-раціональне

 у
у
 | |||||
 | |||||
 |
Х
Лекція 17.
Тема: Показникова функція.
План.
1. Означення показникової функції.
2. Графік показникової функції.
3. Властивості показникової функції.
Функція виду 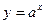 , де
, де  називається показниковою з основою
називається показниковою з основою  .
.
Наприклад:  .
.
у




 |
0 х
Властивості показникової функції:
І. 
1)  .
.
2) Неперервна.
3) Оборотна.
4) Спадна.
5) Графік проходить через точку (0;1).
6) Якщо  , то
, то  . Якщо
. Якщо  , то
, то  .
.
7)  .
.

ІІ. 
1)  .
.
2) Неперервна.
3) Оборотна.
4)Зростаюча.
5) Графік проходить через точку (0;1).
6) Якщо  , то
, то  . Якщо
. Якщо  , то
, то  .
.
7)  .
.
Лекція 18.
Тема: Розв’язування показникових рівнянь, нерівностей.
План.
1.Показникові рівняння.
2.Показникові нерівності.
1.Показникові рівняння.
Показниковими називають рівняння, в яких невідоме входить лише до показників степенів при сталих основах.
Способи розв’язування показникових рівнянь:
1) Зведення до одної основи.
Наприклад: розв’язати рівняння

№174(17;6;19;36) [№1(17;6;19;36)].

2) Винесення спільного множника за дужки. За дужки виносять множник з найменшим показником степеня.
Наприклад: 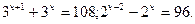
3) Зведення до квадратного рівняння.
Наприклад: 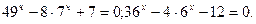
4) Однорідні рівняння і рівняння, що зводяться до однорідних.
Рівняння ділимо почленно на один і той самий вираз.
Наприклад: 
2.Показникові нерівності.
Найпростіші показникові нерівності виду  розв’язують, використовуючи властивості монотонності показникової функції.
розв’язують, використовуючи властивості монотонності показникової функції.
1). Для  >1 з нерівності
>1 з нерівності  випливає
випливає 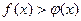 ;
;
з нерівності  маємо
маємо  .
.
2). Для 0 <  <1 з нерівності
<1 з нерівності  випливає
випливає  ;
;
з нерівності  маємо
маємо 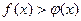 .
.
Наприклад: 
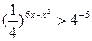 .
.
№ 175(3;9;14;22)
Лекція 19.
Тема: Логарифми.
План.
1. Поняття логарифма.
2. Основна логарифмічна тотожність.
3. Основні властивості логарифмів.
4. Логарифмування.
5. Деякі важливі тотожності, що містять логарифми.
6. Потенціювання.
7. Перехід від однієї основи логарифмів до іншої.
8. Натуральні логарифми.
1.Поняття логарифма.
Показник х степеня  називають логарифмом числа N за основою a.
називають логарифмом числа N за основою a.
Логарифмом числа N за основою а (а>0; а  1) називається показник степеня х, до якого треба піднести а, щоб дістати число N, тт.
1) називається показник степеня х, до якого треба піднести а, щоб дістати число N, тт.  .
.
Зауваження: 1) вираз  має смисл при N>0.
має смисл при N>0.
2) вирази  за основою 10 називають десятковими і позначають
за основою 10 називають десятковими і позначають  .
.
Наприклад:
1) Записати у вигляді логарифмічних рівності 
2) За означенням логарифма перевірити рівності
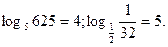
3) Яке число за основою 3 має логарифм 7?
4) За якою основою логарифм числа 10000 дорівнює 4?
5) Знайти логарифм числа  за основою 2.
за основою 2.
6) Знайти основу х, якщо 
 .
.
7) Знайти число х, якщо  .
.
8) За якої основи логарифм числа 3 дорівнює 3?
9) Обчислити  .
.
2.Основна логарифмічна тотожність.
 - основна логарифмічна тотожність.
- основна логарифмічна тотожність.
Наприклад:
1)  .
.
2)Обчислити  .
.
3.Основні властивості логарифмів.

4.Логарифмування.
Прологарифмувати одночлен означає виразити його через логарифми додатних чисел (позначених цифрами і буквами), що входять до його складу.
Наприклад:
Прологарифмувати 
Наприклад:
Обчислити 
5.Деякі важливі тотожності, що містять логарифми.
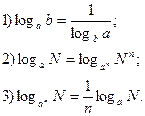
6.Потенціювання-
Перетворення виразу, за допомогою якого за даним логарифмом числа (виразу) визначають саме число (вираз).
Наприклад: Знайти х за логарифмом

7.Перехід від однієї основи логарифмів до іншої.
Нехай  . Треба знайти
. Треба знайти  Про логарифмуємо останню рівність за основою а, маємо
Про логарифмуємо останню рівність за основою а, маємо  .
.
 - формула переходу від однієї основи логарифма до іншої.
- формула переходу від однієї основи логарифма до іншої.
Наприклад: 
8.Натуральні логарифми.
В математичних дослідженнях використовують логарифми за основою, вираженою ірраціональним числом е=2, 718281828… Назву е запропонував Ейлер, а саме число називають на честь шотландського математика Непера неперовим.
Логарифми з основою е називають натуральними і позначають  .
.
Лекція 20.
Тема: Логарифмічна функція, її властивості і графік.
Функція виду 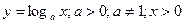 називається логарифмічною за основою а.
називається логарифмічною за основою а.
Оскільки, рівності  визначають за означенням логарифма один і той самий зв’язок між змінними х та у, то показникова і логарифмічна функція є взаємно оберненими, або логарифмічна функція є оберненою до показникової.
визначають за означенням логарифма один і той самий зв’язок між змінними х та у, то показникова і логарифмічна функція є взаємно оберненими, або логарифмічна функція є оберненою до показникової.
Показникові функція відображає зміну степеня числа залежно від зміни показника степеня. Логарифмічна функція відображає зміну показника степеня залежно від зміни степеня числа а.
Графіки показникової та логарифмічної функцій симетричні відносно прямої у=х.

 У у
У у
Y=logax; a>0 Y=logax; 0<a<1
 |  | ||
 1 Х 1 х
1 Х 1 х
Властивості:
1.Д(у)=(0;∞).
2.Е(у)=R.
3.Зростає при a>0; спадає при 0<a<1.
4.Виконуються всі властивості логарифмів.
 5. Під логарифмічні вирази порівнюють з тим самим знаком, що і логарифми при a>0; та з протилежним при 0<a<1.
5. Під логарифмічні вирази порівнюють з тим самим знаком, що і логарифми при a>0; та з протилежним при 0<a<1.
6. Логарифми чисел, більших за одиницю – додатні, менших за одиницю – від’ємні при a>0; і навпаки, логарифми чисел, менших за одиницю – додатні, більших за одиницю – від’ємні при 0<a<1.
7.Зростає х, то зростає і логарифм х при a>0, і, навпаки при 0<a<1.
8.Якщо  , то його логарифм стає від’ємним і як завгодно великим за модулем при a>0; і навпаки при 0<a<1.
, то його логарифм стає від’ємним і як завгодно великим за модулем при a>0; і навпаки при 0<a<1.
Лекція 21.
Тема: Логарифмічні рівняння і нерівності.
Логарифмічним називають рівняння або нерівність, що містять змінну під знаком логарифма.
Наприклад: 
Найпростіше логарифмічне рівняння  ,
,  число, має єдиний розв’язок
число, має єдиний розв’язок  .
.
 Розглянемо рівняння
Розглянемо рівняння  ,
,

Поиск по сайту: