АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Образец выполнения работы

Читайте также:
  1. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  2. Алгоритм выполнения прически
  3. Анализ выполнения договорных обязательств
  4. Анализ выполнения договорных обязательств и реализации продукции
  5. Анализ выполнения федеральной целевой программы «Дети-инвалиды»
  6. Вахтовый метод работы.
  7. Воздушные суда для выполнения рейсов
  8. Время выполнения — 60 минут
  9. Выбор темы и порядок выполнения дипломной работы
  10. Выполнение лабораторной работы.
  11. Выполнение работы.
  12. ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ

В данной работе требуется приближенно вычислить значение заданного интеграла

1.По формуле трапеций с погрешностью , выбрав шаг интегрирования;

2.По формуле Симпсона с шагом h=0.2 и h/2, оценив погрешность найденного значения

Интеграла по правилу Рунге.

Варианты заданий приведены ниже

 

 

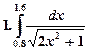
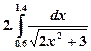
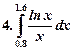
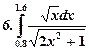
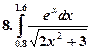
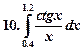
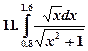
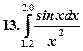
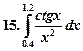
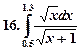
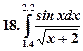
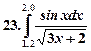
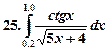
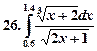
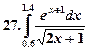
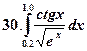
Образец выполнения работы.

 

Вычислить интеграл 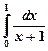с погрешностью по формуле трапеций.

Для решения поставленной задачи сначала найдем шаг интегрирования h. Воспользуемся остаточным членом формулы трапеций для оценки шага. При этом не стоит забывать, что число шагов в формуле трапеций - число целое. Так как модуль разности между точным и приближенным значениями интегралов не превышает модуля остаточного члена, то имеем

и если потребовать чтобы

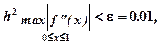
то мы сможем утверждать, что приближенное значение интеграла

найдено с погрешностью

 

Здесь символами 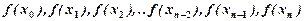обозначены значения подынтегральной функции, вычисленные в точках отстоящих друг от друга на одинаковом расстоянии h.

Выберем шаг численного интегрирования из неравенства

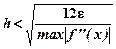, учитывая, что число шагов - целое.

 

Для заданной подынтегральной функции , значит наибольшее значение модуля второй производной будет равно 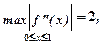а тогда для шага имеем

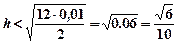, т.е. шаг можно выбрать равным 0.2 (0.2< ).

Составим таблицу значений подынтегральной функции

 

y   1/1.2 1/1.4 1/1.6 1/1.8 1/2
x   0.2 0.4 0.6 0.8  
i            

 

и подставив значения функции в формулу трапеций, получим

 

Итак, приближенное значение интеграла равно 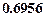, а точное значение:

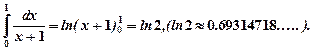Разность точного и приближенного значений интегралов не превышает 0.01.

Для практической оценки погрешности найденного по формуле Симпсона значения интеграла применим правило Рунге. Согласно этому правилу погрешность найденного по формуле Симпсона значения интеграла может быть вычислена по формуле

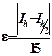, где вычисленные с шагом h и h/2 значения интеграла.

 

Если шаг h = 0.25 (число шагов на отрезке [0,1] равно 4 - четное), то имеем таблицу

y   1/1.25 1/1.5 1/1.75 1/2
x   0.25 0.5 0.75  
i          

 

при h/2= 0.125 (число шагов равно 8) получим таблицу вида

y   1/1.125 1/1.25 1/1.375 1/1.5 1/1.625 1/1.75 1/1.875 1/2
x   0.125 0.25 0.375 0.5 0.625 0.75 0.875  
i                  

 

По формуле Симпсона имеем

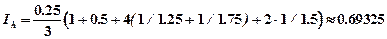
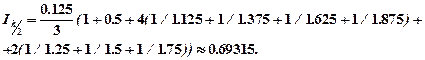
Согласно правилу Рунге практической оценки погрешности получаем

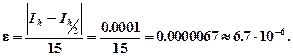
Как следует из формулы, во- первых, значение интеграла 0.69315 найдено с высокой степенью точности, а во- вторых очевидно, что при меньшем числе шагов (большем шаге) формула Симпсона дает более точные результаты, чем формула трапеций.

 


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)