Случайные величины

Пусть дискретная случайная величина X задана таблицей

где р ₁ + р ₂ + … + р _n = 1. (1.3.5)

Математическое ожидание дискретной случайной величины X:

М(X) = . (1.3.6)

(математическое ожидание имеет ту же размерность, что и случайная величина).

Дисперсия дискретной случайной величины X:

D(X) = (1.3.7)

(дисперсия имеет размерность квадрата случайной величины).

Непрерывная случайная величина X может быть задана своей функцией распределения вероятностей или плотностью распределения вероятностей.

Плотность распределения вероятностей случайной величины X:

f _X(x) = f (x) = d P/ dx.

Функция распределения вероятностей случайной величины X:

F _X(x) = F (x) = P (X £ х),

P(x ₁ < X < x ₂) = F (x ₂) – F (x ₁). (1.3.5)

Связь функции распределения и плотности вероятностей:

f (x) = F (x)' = dF (x)/ dx,

F (x) = .

Условие нормировки для непрерывной случайной величины:

= l.

Математическое ожидание непрерывной случайной величины X:

М(Х) = .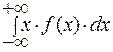

Дисперсия непрерывной случайной величины X:

D(X) = .

Общие соотношения:

D(X) = М{[ Х – М(Х)]²}

или

D(X) = М(Х ²) – [М(Х)]².

Среднее квадратическое отклонение случайной величины:

s (Х) = ÖР(X).

Плотность распределения вероятностей для нормального закона распределения (закона Гаусса):

f (x) = ,

где а – математическое ожидание случайной величины, s – среднее квадратическое отклонение.

Функция распределения вероятностей для нормального закона:

F (x) = Ф(t), (1.3.6)

где t = (х – а)/ s, значения функции Ф(t) даны в соответствующих таблицах.

Плотность распределения вероятностей для равномерного распределения на интервале [ а, b ]:

f (x) = 0 вне отрезка [ а, b ],

f (x) = 1/(b – а) при а £ х £ b.

Плотность вероятности для экспоненциального закона распределения:

f (x) = lехр (– lx), х ³ 0.

Распределение Больцмана:

n = n ₀ exp (– mgh / kT),

где n – концентрация молекул, h – высота над уровнем Земли, m – масса молекулы, k – постоянная Больцмана, g – ускорение свободного падения.

Пример 4. Случайная величина распределена по нормальному закону с нулевым математическим ожиданием (а = 0) и средним квадратическим отклонением а. Найти вероятность того, что эта случайная величина принимает значения в интервалах:

а) – s < X < + s; б) – 2 s < X < + 2 s; в) – 3 s < X < +3 s.

Пример решения для интервала шириной s.

Согласно (1.3.5) и (1.3.6) запишем:

Р(– s < X < + s) = F (s) – F (– s) = Ф[(s – а)/ s ] – Ф[(– s – а)/ s ],

Ф[(s – 0)/ s ] = Ф(1) = 0,8413 (из таблицы),

Ф[(– s – 0)/ s ] = Ф(– 1) = 1 – Ф(1) = 1 – 0,8413 = 0,1587,

Р = Ф (1) – Ф (–1) = 0,8413 – 0,1587 = 0,6826.

Иллюстрация правила трех сигм.

Среди 10 000 значений нормальной случайной величины в среднем только 27 выйдут за пределы интервала (а – 3 s, а + 3 s). Это означает, что среди небольшого числа значений X практически нет таких, которые выходят за пределы указанного интервала.

Пример 5. Случайная величина X распределена по нормальному закону с математическим ожиданием 3 и дисперсией 4. Найти вероятность того, что 1 < X < 7.

Решение. а = 3, s = Ö4 = 2 найдем искомую вероятность (без вывода):

Р(1< X < 7) = [Ф{(7 – 3)/2} – Ф{(1 – 3)/2}] = [Ф(2) – Ф(–1)] =

= (0,9772 – 0,1587) = 0,8185.

Поиск по сайту: