Tools for Power Measurement

Power is typically measured with a digital power analyzer or a DSO (digital storage oscilloscope) with power-analysis firmware. Most modern power analyzers are entirely electronic and use digitizers to convert analog signals to digital forms. Higher end analyzers use digital signal processing techniques to make the calculations required to determine values.

As explained above, different methods can be used to calculate the reactive power. The theoretical definition of the reactive power is difficult to implement in an electronic system at a reasonable cost. It requires a dedicated DSP to process the Hilbert transform necessary to get a constant phase shift of 90° at each frequency. Several solutions have been developed to overcome this limitation. They can be categorized in three groups:

1- Method 1: Power triangle
The Power triangle method is based on the assumption that the three energies, apparent, active and reactive, form a right-angle triangle as shown in Figure 1. The reactive power can

(6)

then be processed by estimating the active and apparent energies and applying:
Although this method gives excellent results with pure sinusoidal waveforms, noticeable errors appear in presence of harmonics (Table 1).

2- Method 2: Time delay
A time delay is introduced to shift one of the waveforms by 90° at the fundamental frequency and multiply the two waveforms:

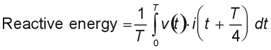(7)

where T is the period of the fundamental. In an electronic DSP system, this method can be implemented by delaying the samples of one input by the number of samples representing a quarter-cycle of the fundamental frequency (Fline) (Figure 2)

This method presents drawbacks if the line frequency changes and the number of samples no longer represents a quarter-cycle of the fundamental frequency. Significant errors are then introduced to the results (Table 1).

3- Method 3: Low-pass filter
A constant 90° phase shift over frequency with an attenuation of 20 dB/decade is introduced. This solution, which has been implemented by Analog Devices, can be realized with a single pole low-pass filter on one channel input (Figure 3). If the cut-off frequency of the low-pass filter is much lower than the fundamental frequency, this solution provides a 90° phase shift at any frequency higher than the fundamental frequency. It also attenuates these frequencies by 20 dB/decade (Figure 4).

Similarly to method 2, this solution is susceptible to variations of the line frequency. However, a dynamic compensation of the gain attenuation with the line frequency can be achieved by evaluating the line period of the signal.

There are several power equations relating the three types of power to resistance, reactance, and impedance (all using scalar quantities):

Please note that there are two equations each for the calculation of true and reactive power. There are three equations available for the calculation of apparent power, P=IE being useful only for that purpose. Examine the following circuits and see how these three types of power interrelate for: a purely resistive load in Figure belw, a purely reactive load in Figure belw, and a resistive/reactive load in Figure belw.

Resistive load only:

True power, reactive power, and apparent power for a purely resistive load.

Reactive load only:

True power, reactive power, and apparent power for a purely reactive load.

Resistive/reactive load:

True power, reactive power, and apparent power for a resistive/reactive load.

These three types of power -- true, reactive, and apparent -- relate to one another in trigonometric form. We call this the power triangle: (Figure belw).

Power triangle relating appearant power to true power and reactive power.

Using the laws of trigonometry, we can solve for the length of any side (amount of any type of power), given the lengths of the other two sides, or the length of one side and an angle.

REVIEW:

· Power dissipated by a load is referred to as true power. True power is symbolized by the letter P and is measured in the unit of Watts (W).

· Power merely absorbed and returned in load due to its reactive properties is referred to as reactive power. Reactive power is symbolized by the letter Q and is measured in the unit of Volt-Amps-Reactive (VAR).

· Total power in an AC circuit, both dissipated and absorbed/returned is referred to as apparent power. Apparent power is symbolized by the letter S and is measured in the unit of Volt-Amps (VA).

· These three types of power are trigonometrically related to one another. In a right triangle, P = adjacent length, Q = opposite length, and S = hypotenuse length. The opposite angle is equal to the circuit's impedance (Z) phase angle.

Поиск по сайту: