 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Напряженность и потенциал электростатического поля. Связь между ними. Энергия взаимодействия системы зарядов
Потенциал φ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.
Из формул (4) и (2) следует, что потенциал поля, создаваемого точечным зарядом Q, равен
 (5)
(5)
Работа, которую совершают силы электростатического поля при перемещении заряда Q0 из точки 1 в точку 2 (см. (1), (4), (5)), может быть выражена как
 (6)
(6)
т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, которая совершается силами поля, при перемещении единичного положительного электрического заряда из точки 1 в точку 2.
Работа сил поля при перемещении заряда Q0 из точки 1 в точку 2 может быть выражена как
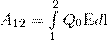 (7)
(7)
Приравняв (6) и (7), придем к формуле для разности потенциалов:
 (8)
(8)
где интегрирование можно производить вдоль любой линии, которая соединяет начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.
Если перемещать заряд Q0 из произвольной точки за далеко пределы поля, т. е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (6), A∞=Q0φ, откуда
 (9)
(9)
Значит, потенциал — физическая величина, которая определяется работой по перемещению единичного положительного электрического заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, которую совершают внешние силы (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.
Из выражения (4) видно, что единица потенциала — вольт (В): 1 В равен потенциалу такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная ранее единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл=1 Н•м/(Кл•м)=1 Дж/(Кл•м)=1 В/м.
Из формул (3) и (4) следует, что если поле создается несколькими зарядами, то потенциал данного поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, которая действует на пробный единичный положительный заряд, помещенный в эту точку поля:
 (1)
(1)
Как следует из формулы (1) и закона Кулона, напряженность поля точечного заряда в вакууме
 или
или  (2)
(2)
Направление вектора Е совпадает с направлением силы, которая действует на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду (рис. 1).
Из формулы (1) следует, что единица напряженности электростатического поля — ньютон на кулон (Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл= 1 В/м, где В (вольт) — единица потенциала электростатического поля.

Рис.1
Графически электростатическое поле представляют с помощью линий напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис. 2). Линиям напряженности задается направление, которое совпадает с направлением вектора напряженности. Поскольку в любой данной точке пространства вектор напряженности имеет только одно направление, то линии напряженности не могут пересекаться. Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) все линии напряженности параллельны одному вектору напряженности. Если электрическое поле создается точечным зарядом, то линии напряженности — радиальные прямые, которые выходят из заряда, если он положителен (рис. 3, а), и которые входят в него, если заряд отрицателен (рис. 3, б).

Чтобы с помощью линий напряженности можно задавать не только направление, но и численное значение напряженности электростатического поля. Условились рисовать их с определенной густотой (см. рис. 2): число линий напряженности, которые пронизывают единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, которые пронизывают элементарную площадку dS, нормаль n которой образует угол α с вектором Е, равно ЕdScosα = EndS, где Еn — есть проекция вектора Е на нормаль n к площадке dS (рис. 4). Величина

называется потоком вектора напряженности через площадку dS. Здесь d S = dS n — вектор, у которого модуль равен dS, а направление совпадает с направлением нормали n к площадке. Выбор направления вектора n (а следовательно, и db>S) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля — 1 В•м.
Для произвольной замкнутой поверхности S поток вектора Е сквозь данную поверхность
 (3)
(3) 
Рис.4
где интеграл мы берем по замкнутой поверхности S. Поток вектора Е является алгебраической величиной: зависит не только от свойств поля Е, но и от выбора направления n. Для замкнутых поверхностей положительным направлением нормали считается внешняя нормаль, т. е. нормаль, которая направлена наружу области, охватываемой поверхностью.
| |
|
Теорема Гаусса для напряженности электростатического поля. Применения теоремы Гаусса для вычисления напряженности электростатического поля: а) заряженной сферической поверхности, б) бесконечной однородно заряженной плоскости, в) равномерно заряженной бесконечно длинной нити.
Задачу вычисления напряженности поля системы электрических зарядов, используя помощью принципа суперпозиции электростатических полей можно сильно облегчить, если применять открытую немецким ученым К. Гауссом (1777—1855) теорему, которая определяет поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность.
Из определения потока вектора напряженности сквозь замкнутую поверхность, поток вектора напряженности сквозь сферическую поверхность радиуса r, которая охватывает точечный заряд Q, находящийся в ее центре (рис. 1), равен

Этот результат справедлив для замкнутой поверхности произвольной формы. Действительно, если заключить сферу (рис. 1) в произвольную замкнутую поверхность, то каждая линия напряженности, которая пронизывает сферу, пройдет и сквозь эту поверхность.
В случае, если замкнутая поверхность любой формы охватывает заряд (рис. 2), то при пересечении любой линии напряженности с поверхностью она то входит в нее, то выходит из нее. При вычислении потока нечетное число пересечений в конечном счете сводится к одному пересечению, так как поток полагается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, которые входят в поверхность.

Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, которые входят в поверхность, равно числу линий напряженности, которые выходят из нее.
Значит, для поверхности произвольной формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/ε0, т. е.
 (1)
(1)
Знак потока совпадает со знаком заряда Q.
Исследуем общий случай произвольной поверхности, окружающей n зарядов. Используя с принцип суперпозиции, напряженность Е поля, которая создавается всеми зарядами, равна сумме напряженностей Ei полей, которые создаваются каждым зарядом в отдельности. Поэтому

Согласно (1), каждый из интегралов, который стоит под знаком суммы, равен Qi/ε0. Значит,
 (2)
(2)
Формула (2) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε0. Эта теорема получена математически для векторного поля произвольной природы русским математиком М.В.Остроградским (1801—1862), а затем независимо от него применительно к электростатическому полю — К. Гауссом.
В общем случае электрические заряды могут быть распределены с некоторой объемной плотностью ρ=dQ/dV, которая различна в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, которая охватывает некоторый объем V,
 (3)
(3)
Используя формулу (3), теорему Гаусса (2) можно записать так:

А) Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +σ. Т.к. заряд распределен равномернопо поверхности то поле, которое создавается им, обладает сферической симметрией. Значит линии напряженности направлены радиально (рис. 3). Проведем мысленно сферу радиуса r, которая имеет общий центр с заряженной сферой. Если r>R,ro внутрь поверхности попадает весь заряд Q, который создает рассматриваемое поле, и, по теореме Гаусса, 4πr2E = Q/ε0, откуда
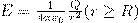 (3)
(3)
При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости Е от r приведен на рис. 4. Если r'<R, то замкнутая поверхность не содержит внутри себя зарядов, значит внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E=0).

Б) Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 1) заряжена с постоянной поверхностной плотностью +σ (σ = dQ/dS — заряд, который приходится на единицу поверхности). Линии напряженности перпендикулярны данной плоскости и направлены от нее в каждую из сторон. Возьмем в качестве замкнутой поверхности цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности поля (соsα=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Еn совпадает с Е), т. е. равен 2ES. Заряд, который заключен внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Гаусса, 2ES=σS/ε0, откуда
 (1)
(1)
Из формулы (1) следует, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях равна по модулю, иными словами, поле равномерно заряженной плоскости однородно.
В) Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 6) равномерно заряжен с линейной плотностью τ (τ = –dQ/dt заряд, который приходится на единицу длины). Из соображений симметрии мы видим, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. Мысленно построим в качестве замкнутой поверхности коаксиальный цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы и линии напряженности параллельны), а сквозь боковую поверхность равен 2πr l Е. Используя теорему Гаусса, при r>R 2πr l Е = τ l /ε0, откуда
 (5)
(5)
Если r<R, то замкнутая поверхность внутри зарядов не содержит, поэтому в этой области E=0. Значит, напряженность поля вне равномерно заряженного бесконечного цилиндра задается выражением (5), внутри же его поле равно нулю.

Поиск по сайту:
 (1) где символ частной производной подчеркивает, что дифференцирование осуществляется только по х. Повторив эти рассуждения для осей у и z, найдем вектор Е:
(1) где символ частной производной подчеркивает, что дифференцирование осуществляется только по х. Повторив эти рассуждения для осей у и z, найдем вектор Е:  где i, j, k — единичные векторы координатных осей х, у, z. Из определения градиента следует, что
где i, j, k — единичные векторы координатных осей х, у, z. Из определения градиента следует, что 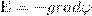 или
или  (2) т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус говорит о том, что вектор напряженности Е поля направлен в сторону уменьшения потенциала. Для графического представления распределения потенциала электростатического поля, как и в случае поля тяготения, пользуютсяэквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал φ имеет одинаковое значение. Если поле создается точечным зарядом, то его потенциал, согласно формуле потенциала поля точечного заряда, φ=(1/4πε0)Q/r.Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы с цетром в точечном заряде. Заметим также, линии напряженности в случае точечного заряда — радиальные прямые. Значит, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям. Линии напряженности всегда перпендикулярны к эквипотенциальным поверхностям. В самом деле, все точки эквипотенциальной поверхности обладают одинаковым потенциалом, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, которые действуют на заряд, всегда направлены по перпендикурярам к эквипотенциальным поверхностям. Значит, вектор Е всегда перпендикулярен к эквипотенциальным поверхностям, а поэтому линии вектора Е перпендикулярны этим поверхностям. Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесконечное множество. Но обычно их проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были равны друг другу. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где гуще расположены эти поверхности, напряженность поля больше. Значит, зная расположение линий напряженности электростатического поля, можно нарисовать эквипотенциальные поверхности и, наоборот, по известному нам расположению эквипотенциальных поверхностей можно найти в каждой точке поля направление и модуль напряженности поля. На рис. 1 в качестве примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного электрического заряда (а) и заряженного металлического цилиндра, который имеет на одном конце выступ, а на другом — впадину (б).
(2) т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус говорит о том, что вектор напряженности Е поля направлен в сторону уменьшения потенциала. Для графического представления распределения потенциала электростатического поля, как и в случае поля тяготения, пользуютсяэквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал φ имеет одинаковое значение. Если поле создается точечным зарядом, то его потенциал, согласно формуле потенциала поля точечного заряда, φ=(1/4πε0)Q/r.Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы с цетром в точечном заряде. Заметим также, линии напряженности в случае точечного заряда — радиальные прямые. Значит, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям. Линии напряженности всегда перпендикулярны к эквипотенциальным поверхностям. В самом деле, все точки эквипотенциальной поверхности обладают одинаковым потенциалом, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, которые действуют на заряд, всегда направлены по перпендикурярам к эквипотенциальным поверхностям. Значит, вектор Е всегда перпендикулярен к эквипотенциальным поверхностям, а поэтому линии вектора Е перпендикулярны этим поверхностям. Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесконечное множество. Но обычно их проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были равны друг другу. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где гуще расположены эти поверхности, напряженность поля больше. Значит, зная расположение линий напряженности электростатического поля, можно нарисовать эквипотенциальные поверхности и, наоборот, по известному нам расположению эквипотенциальных поверхностей можно найти в каждой точке поля направление и модуль напряженности поля. На рис. 1 в качестве примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного электрического заряда (а) и заряженного металлического цилиндра, который имеет на одном конце выступ, а на другом — впадину (б).
