Способ сложения

Основная идея способа - преобразовать систему так, чтобы в одном из уравнений осталась одна неизвестная величина. Этого можно достичь подстановкой, а можно почленным сложением уравнений системы. Рассмотрим данный способ также на примерах.

Пример 1. Решить систему:

Сложим почленно два уравнения системы, получим . Для определения подставим найденное значение в любое из уравнений системы, например, в первое: , откуда .

Ответ: .

Пример 2. Решить систему:

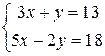
Преобразуем систему, умножив обе части первого уравнения на 2:

Теперь почленно сложим оба уравнения, получим , откуда . Подставив это значение в первое уравнение, найдем .

Ответ: .

Замечание. В некоторых случаях при решении систем линейных уравнений можно использовать приемы, чаще применяемые при решении нелинейных систем.

Пример. Решить систему линейных уравнений:

Прибавим ко второму уравнению системы первое, умноженное на –2, получим однородное уравнение , из которого выразим и подставим полученное соотношение в первое уравнение, найдем:

3.3. Метод Гаусса

Этот метод является продолжением и обобщением рассматриваемых школе методов подстановки и сложения.

Запишем систему так, чтобы в первом уравнении при первом неизвестном коэффициент был равен 1. Если в системе есть подходящее уравнение, его можно переставить на первое место, если такого уравнения нет, то обе части первого уравнения можно разделить на коэффициент при первом неизвестном (полагая, конечно, что он отличен от 0). Умножая последовательно первое уравнение на числа, противоположные коэффициентам при первом неизвестном в остальных уравнениях, прибавляем его ко второму, третьему и т.д. уравнениям системы.

После этого во всех уравнениях системы, кроме первого, первое неизвестное будет исключено, т.е. эти уравнения будут содержать на одно неизвестное меньше, да и самих уравнений будет на одно меньше (первое не рассматриваем). Значит, эти уравнения образуют систему уравнений на порядок меньше, чем в исходной. С этой системой можно провести такие же преобразования, как на первом этапе и т.д. до тех пор, пока в одном уравнении не останется одно неизвестное. Рассмотрим примеры.

Пример 1. Решить систему линейных уравнений

Поменяем местами первое и второе уравнения системы:

Выполним такие преобразования: ко второму уравнению системы прибавим первое, умноженное на (-3), к третьему – первое, умноженное на (-2). После выполнения указанных действий система примет вид:

Умножив второе уравнение на (-1), прибавим его к третьему, тогда:

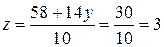Из последнего уравнения находим , из второго ; из первого . Подстановкой найденных значений во все уравнения исходной системы убеждаемся, что они являются ее решением.

Пример 2. Решить систему линейных уравнений

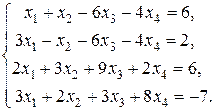
Умножая первое уравнение на (-3) и прибавляя ко второму, затем на (-2) и прибавляя к третьему, затем на (-3) и прибавляя к четвертому, преобразуем систему.

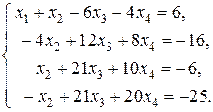
Предварительно разделив обе части второго уравнения на (-4), прибавим его к четвертому уравнению, умножив на (-1), прибавим к третьему, тогда:

Разделим обе части третьего уравнения на 12, а четвертого - на 3, затем третье уравнение, умноженное на (-3), прибавим к четвертому, получим:

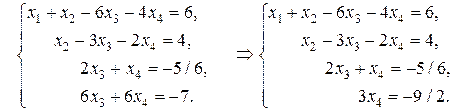
Из последнего уравнения находим 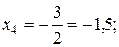из третьего ; из второго ; из первого . Подставляем найденные значения во все уравнения системы и убеждаемся, что решение верно.

Решение систем линейных уравнений по методу Гаусса особенно удобно, когда коэффициенты при неизвестных целые числа, в тех случаях, когда коэффициенты произвольны или даны в общем виде, решение системы (особенно вручную) по методу Гаусса может представлять непростую задачу. Попробуем найти еще один способ решения систем линейных уравнений.

Поиск по сайту: