Нахождение обратной матрицы

Используя различные действия с матрицами, можно составлять матричные уравнения: соотношения между неизвестной матрицей Х и известными матрицами, записанные в виде равенства.

Например, АХ = В или ХА = В, АХВ = С, АХ + В = С, ХА — В = С и т.д.

Рассмотрим одно из простейших матричных уравнений: .

В школьном курсе алгебры рассматривалось соответствующее ему уравнение для действительных чисел: .

Решением этого линейного уравнения является , где число называется обратным к 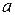и удовлетворяет соотношению: .

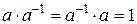Введем подобное понятие и для матриц. Матрица называется обратной к , если она удовлетворяет условию:

,

где — единичная матрица.

Из определения обратной матрицы следует, что ее можно найти только для квадратных матриц.

Существование обратной матрицы дает возможность решать матричные уравнения, например, рассмотрим уравнение . Умножим обе части уравнения слева на матрицу, обратную :

.

Аналогично можно найти решение уравнения , умножая теперь уже справа обе части уравнения на :

.

Для уравнения решением будет .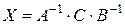

Рассмотрим способы нахождения обратной матрицы.

Поиск по сайту: