Алгоритм оценки погрешностей прямых измерений физических величин

Как ранее отмечено, погрешности прямых измерений могут быть однократными (выполняют одно измерение) или – многократными (выполняют несколько измерений).

Однократные измерения применяют в том случае, если измеряемая величина и допускаемая ее погрешность заранее известны и их определение выполнено по аттестованной методике. Это своего рода контрольные измерения. Если разница между нормированным и измеренным значениями не превышает допускаемой погрешности, то результат считают положительным и полученное опытным путем значение используют при сертификации продукции.

Наиболее сложный случай возникает, когда значения физической величины и ее погрешности заранее не известны. В этом случае приходится прибегать к многократным измерениям.

Пусть в результате многократных измерений величины Х получено п результатов наблюдений:

При этом применено техническое средство измерения с приборной (систематической) погрешностью Х _сист.

Необходимо с доверительной вероятностью Р 0,95 определить измеренное значение величины Х и ее доверительный интервал.

По этим данным вычисляют среднее арифметическое значение, которое считают наилучшим приближением к истинному значению измеряемой величины:

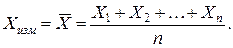
Приведенных данных достаточно для вычисления среднеквадратической погрешности результата измерений этого среднего арифметического значения:

С помощью таблицы (приложение 3) по численным значениям Р и n находят величину и вычисляют доверительный интервал отклонения случайной величины от измеренного значения:

Поскольку при проведении экспериментов обычно выполняют не более 5-10 измерений, то величины случайной и приборной (систематической) погрешностей близки друг к другу и обе они в равной степени определяют точность измерений. Поэтому суммарная погрешность измерения Х должна быть определена с учетом этого обстоятельства:

Однако при вычислении Х предварительно целесообразно сравнить между собой величины случайной ( Х_сл) и систематической (приборной) Х_пр погрешностей. Можно отбросить, как незначительную, ту из погрешностей, которая меньше другой в три и более раз:

если то

если то

Если приведенные неравенства не выполняются, то обе погрешности значимы и за суммарную погрешность принимаем:

Так как – максимальная погрешность прибора, то можно утверждать, что доверительный интервал в этом случае оценивается с вероятностью, по крайней мере, не меньшей, чем 0,954, если оценивается этой же вероятностью.

Полученный результат измерения обычно представляют в следующем виде:

Возможны и другие формы представления полученного результата, но в любом случае принято указывать не относительную, а абсолютную погрешность.

Полученные численные значения среднеарифметического результата измерения и его погрешности следует представить в соответствии с действующими правилами (стандарт СТ СЭВ 543-77), суть которых сводится к следующему:

1. Погрешность должна содержать не более двух значащих цифр. При этом значащими цифрами считают все цифры от первой слева, не равной нулю, до последней цифры, в том числе, считая нули, которыми заканчивается число. Нули, следующие из множителя 10 ⁿ, во внимание не принимают.

Примеры определения количества значащих цифр в числах:

12,0 имеет 3 значащих цифры (включая нуль);

30 имеет 2 значащих цифры (включая нуль);

(120×10³) имеет 3 значащих цифры (включая нуль и не считая множителя 10³);

(0,514×10²) имеет 3 значащих цифры (не считая нуль слева и множителя 10²);

0,0056 имеет 2 значащих цифры (не считая двух нулей слева).

2. Нельзя вычислять искомую величину до пяти, шести, а иногда и более значащих цифр. Следует понимать, что эта точность иллюзорна.

Если хотя бы одна из величин, в каком-либо сложном выражении задана с точностью до двух значащих цифр (не считая нулей впереди), то нет смысла вести вычисление результата с точностью более, чем до двух значащих цифр. Иначе говоря, численное значение результата не должно содержать большего количества цифр, чем в числе, заданном с наименьшей точностью.

Следует помнить, что точность результата не является самоцелью,
а зависит от практической потребности в ней (удобства производства и эксплуатации любой продукции).

3. Количество разрядов в числах результата и погрешности должно быть одинаково.

Примеры правильных и неправильных записей:

17,0 0,2 – правильно (количество разрядов после запятой одинаковое);

17,01 0,2 – неправильно (количество разрядов после запятой неодинаковое: результат измерения имеет точность до сотых, а погрешность до десятых);

17,0 0,22– неправильно (количество разрядов после запятой неодинаковое: результат измерения имеет точность до десятых, а погрешность до сотых).

4. Следует различать записи приближенных чисел по количеству значащих цифр.

Пример: 2,4 и 2,40.

В первом случае (2,4) верны только цифры целых и десятых, т. е. возможны и другие значения истинного числа, в том числе: 2,38; 2,43.

Во втором случае (2,40) верны целые, десятые и сотые. Истинные значения могут иметь следующие значения: 2,403 и 2,398, но не 2,421 или 2,382.

5. При вычислениях неизбежны округления чисел до нужного количества значащих цифр или разрядов.

Основные правила выполняемых при этом операций сводятся
к следующему:

округление чисел до желаемого количества значащих цифр следует выполнять сразу, а не по этапам.

Например, необходимо число 565,46 округлить до 3-х значащих цифр. Правильным будет результат 565.

Если же округления проводить поэтапно, то получим следующее: на первом этапе 565,46 округлим до 565,5. Затем 565,5 до 566. Из полученного результата и сравнения его с первоначальным значением видно, что он оказался завышенным;

округление чисел до желаемого количества разрядов следует выполнять по правилам математики.

6. Целые числа округляют по тем же правилам, что и дробные.
Например, число 12456 надо округлить до двух значащих цифр. Правильным будет результат 12×10³.

5. Задачи и вопросы для самоконтроля

Дайте определения понятиям абсолютной и относительной погрешности измерений. В каких единицах они измеряются?

В каких случаях можно пренебречь систематической или случайной погрешностями при вычислении суммарной ошибки измерения?

Что понимают под количеством измерений и степенью свободы?

В чем принципиальное сходство и разница между распределениями ошибок по нормальному закону и по Стьюденту?

Что понимают под доверительной вероятностью и доверительным интервалом результата измерения?

В чем состоит алгоритм определения коэффициента Стьюдента при выполнении расчетов погрешности измерения?

Каков порядок округления результатов расчета погрешности измерений?

Какие рекомендуются формы представления результатов расчета погрешности измерения?

Раскройте сущность правила определения количества значащих цифр в числе.

До какого количества значащих цифр рекомендуется округлять погрешность измерений?

Порядок согласования количества разрядов в числах, соответствующих рассчитываемой величине и ее погрешности.

Сущность нормального закона и распределения Стьюдента применительно к ошибкам измерений.

Понятия о доверительном интервале измеряемой физической величины и доверительной вероятности нахождения ее в этом интервале.

Что понимают под точностью, погрешностью и доверитель-ностью результатов измерений?

Какое значение измеряемой величины следует принять за истинное, если оно заранее неизвестно? Как его найти?

Какой физический смысл заложен в русской пословице «Семь раз отмерь, один раз отрежь»?

Перепишите следующие ответы в наиболее наглядном виде
с нужным числом значащих цифр:

а) измеренная высота = 5,033±0,04329 м;

б) измеренное время = 19,5432±1 с;

в) измеренный заряд = -3,21×10^-19±2,67×10^-20 Кл;

г) измеренная длина волны = 0,000000563±0,00000007 м;

д) измеренный импульс =3,267×10³±42

Студент измеряет плотность жидкости пять раз и получает результаты в : 1,8; 2,0; 2,0; 1,9; 1,8. Что вы могли бы предположить о наилучшей оценке и погрешности измерений, основываясь на результатах измерений?

а) Калькулятор студента показывает результат 123,123. Если студент решил, что это число в действительности имеет только три значащие цифры, оцените каковы его абсолютная и относительная погрешности.

б) Сделайте то же для числа 0,123123.

в) Сделайте то же для числа 321,321.

г) Лежит ли относительная погрешность в интервале, ожидаемом для случая трех значащих цифр?

Посетитель средневекового замка решает определить глубину колодца, измеряя время падения брошенного в него камня. Он определяет, что время падения равно t = 3,0±0,5 с. Какой вывод он сделает о глубине колодца?

Поиск по сайту: