АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вопрос 2. Построение доверительного интервала при неизвестном законе генерального распределения

Читайте также:
  1. II. Вопросительное предложение
  2. VII. Вопросник для анализа учителем особенностей индивидуального стиля своей педагогической деятельности (А.К. Маркова)
  3. X. примерный перечень вопросов к итоговой аттестации
  4. Аграрный вопрос
  5. Антиполия-противоречие в в законе. Противоречие разрешаясь делает чего то возможным. Отрицание-отрицания ( разрешение противоречия (синтез))
  6. Болгарский вопрос. Соборы на Западе на Востоке. Окончательное разделение 1054 года
  7. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 1 страница
  8. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 1 страница
  9. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 1 страница
  10. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 10 страница
  11. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 10 страница
  12. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 11 страница

Пусть количественный признак Х генер совок-ти распределен нормально, причем с.к.о. этого распределения известно, требуется оценить неизвестное мат ожидание, а выборочная средняя ̅̅Х. Поставим задачей построение доверительного интервала, покрывающего параметры а, с надежностью у.

Будем рассматривать выборочную среднюю ̅̅Х как случ величину х и выборочное значение признака х1, х2,…хn - как одинаково распределенные независимые случ величины х1, х2,…хn. Мат ожидание каждой из этих величин равно а, и с.к.о. – Ϭ. М(̅̅Х)=а и Ϭ(̅̅Х)= Ϭ/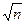

Можно записать Р((̅̅Х-а) < tϭ/ 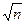)=2Ф(t). Применив во внимание, что вероятность Р задана и равна ̅̅У – окончательно имеем: Р(̅̅х= tϭ/ 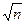<а< ̅̅х+tϭ/ 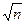) =2Ф(t)= ̅̅у. Показывая неизвестный параметр а, точность оценки Ϭ= tϭ/ 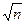. число t определяется из равенства 2Ф(t)=у, Ф(t)=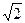

Ф-ции Лапласа находят аргумент t, который соответствует значению ф-ции Лапласа.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)